Лекция 02. Теория булевых функций. Булева алгебра
Определение.
Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (Аксиомы булевой алгебры). Названия операций пока не введены.
1. X & Y = Y&X, X V Y = Y V X – коммутативность.
2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.
3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.
4. Поглощение – X & X = X, X V X = X.
5. Свойства констант
X & 0 = 0
X & I = X, где I – аналог универсального множества.
6. Инвальтивность (X*)* = X
7. Дополнимость X V X* = I, X & X* = 0.
8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y
Булева алгебра всех подмножеств данного множества.
U = {a1, a2… an)
[U] = N
[P(U)] = 2n
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, Множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Oбъединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I.
Все аксиомы булевой алгебры справедливы в операциях над множествами.
Булева алгебра характеристических векторов.
Пусть A <= U, A <- P(U) a- характеристический вектор этого подмножества.
AA = {a, a2 ..an)
N = [P(U)]
Ai = 1, если ai <- A (принадлежит).
Ai = 0, если ai не принадлежит A.
U = {1 2 3 4 5 6 7 8 9}
A = {2 4 6 8}
B = {1 2 7}
AA = {0 1 0 1 0 1 0 1 0}
AB = {1 1 0 0 0 0 1 0 0}
Или
AA = 010101010 – скобки не нужны
AA= 110000100
Характеристические векторы размерностью n называются булевыми векторами.
Они располагаются в вершинах n – мерного булева куба.
Номером булевого вектора является число в двоичном представлении, которым он является
1101 – номер.
Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (если они отличаются только одной координатой).
Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bn.
Булев куб размерности 1

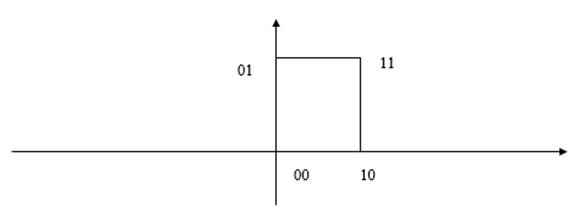
Булев куб размерности 2
Булев куб размерности 3
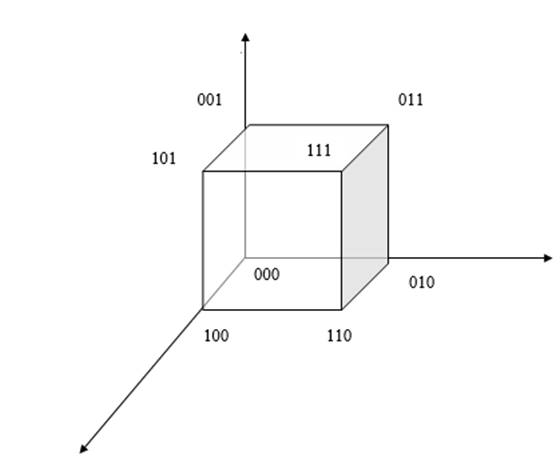
0 – нулевой вектор.
I – вектор из одних единиц.

Отрицание
X = 0 Y = 0
_ _
Х = 1 Y= 1
Для размерности n операции над векторами производятся покоординатно.
Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.
Утверждение
Между множеством всех подмножеств множества U и булевым кубом Bn, где n= =[U] можно установить взаимное соответствие, при котором операции объединения множества соответствует операции логического сложения (их характеристических векторов), операции пересечения множеств соответствует операция логического умножения их характеристических векторов, а операции дополнения – операция отрицания. Пустому множеству соответствует нулевой вектор, а универсальному – единичный.
Следствие
Множество всех характеристических векторов является булевой алгеброй.
Булева алгебра высказываний (алгебра логики)
Высказыванием об элементах множества U называется любое утверждение об элементах множества U, которое для каждого элемента либо истинно, либо ложно.
U = {1 2 3 4 5 6 7 8 9}
A = «число четное»
B = «число, меньшее пяти»
Множеством истинности высказывания называется совокупность всех элементов, для которых это высказывание истинно.
SA = {2 4 6 8}
SB = {1 2 3 4}
Высказывание, для которого множество истинности пусто, называется тождественно ложным, а для которого SB = U называется тождественно истинным.
Высказывания, для которых множества истинности совпадают, называются тождественными или равносильными.
Равносильные высказывания объединим в один класс Р. В. и не будем их разделять, т. к. все они имеют одно и то же множество истинности.
Операции над высказываниями
Дизъюнкция высказываний (V, ИЛИ, OR)
Дизъюнкция высказываний – высказывание, истинное тогда, когда истинно хотя бы одно из высказываний.
Конъюнкция высказываний (&, И, AND).
Конъюнкцией высказываний называется высказывание, истинное тогда и только тогда, когда истинны все высказывания.
Отрицание высказываний (- над буквой, НЕ, NOT).
Отрицанием высказывания называется высказывание, истинное только тогда, когда исходное высказывание ложно.
|
A B |
A & B |
A V B |
Not A |
|
Л Л |
Л |
Л |
И |
|
Л И |
Л |
И |
И |
|
И Л |
Л |
И |
Л |
|
И И |
И |
И |
Л |
Л – ложно.
И – истинно.
Утверждение (основа всей алгебры логики)
Между множеством всех классов эквивалентных высказываний об элементах множества U и множеством P(U) можно установить взаимно однозначное соответствие, при котором операция дизъюнкции высказываний соответствует операции объединения множеств истинности, а конъюнкция соответствует операции пересечения. Операция отрицания соответствует операции дополнения.
Следствие. Множество классов эквивалентных высказываний является булевой алгеброй.
Теорема
Существуют 3 булевых алгебры:
1. P(U)
2. Bn
3. Множество классов эквивалентных высказываний.
Три булевых алгебры являются изоморфными, если между их элементами можно установить такое однозначное соответствие, при котором операции сохраняются.
Договоримся конъюнкцию обозначать точкой (как знак умножения в алгебре чисел). Конъюнкция выполняется раньше дизъюнкции (аналог выполнения операций сложения и умножения в алгебре чисел).
| < Предыдущая | Следующая > |
|---|