17. Две задачи из теории плоских кривых

Рассмотрим плоскую кривую, параметризованную натуральным параметром . В этом случае касательный вектор и вектор нормали образуют подвижный репер в плоскости, в которой лежит кривая. Уравнения Френе имеют вид: ,

откуда получаем систему дифференциальных уравнений второго порядка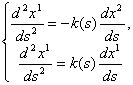

Овалом называют плоскую замкнутую линию, не имеющую ни с какой прямой больше двух общих точек. Область, которую ограничивает овал, очевидно, выпукла и кривизна овала во всех его точках положительна. Назовем Вершиной овала точку, в которой производная меняет знак. Докажем теорему о четырех вершинах овала, впервые найденную, по-видимому бенгальским математиком S. Mukhopadhyaya.

Теорема. Овал имеет не менее четырех вершин.

В доказательстве будет использовано интегральное равенство , при произвольных постоянных . Равенство следует из следующих трех других : 1)

2)

3) которое получается аналогично 2).

Справедливость всех трех вытекает из замкнутости овала. Мы предполагаем функцию класса , поэтому наверное найдутся наименьшее и наибольшее значения , и значит, существуют по меньшей мере две вершины, где . Но если бы имелись только эти вершины, то мы могли бы провести через них прямую и интегральное равенство не имело бы места, так как подынтегральное выражение не меняло бы знак. При этом мы использовали тот факт, что линия является овалом. Трех вершин также не может быть, поскольку исследуя интервалы монотонности функции , легко прийти к противоречию.

Таким образом, на овале должно происходить по меньшей мере четыре перемены знака производной .

< Предыдущая		Следующая >