18. Основное изопериметрическое свойство круга

Между длиной и площадью плоской области существует изопериметрическое соотношение , причем равенство выполняется только в том случае, если является кругом (единственность). Таким образом, при заданной длине площадь достигает своего максимального значения только в случае круга. Известно более десяти различных доказательств этого факта. Мы приведем доказательство, принадлежащее A. Hurwitz’у. Оно предполагает, что граница области представляет собой кусочно-гладкую кривую.

Пусть периодические функции (с периодом ) являются декартовыми координатами точки, описывающей замкнутую линию . Положим . Рассмотрим два ряда Фурье .

Отсюда следует

.

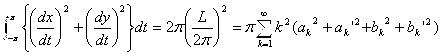Для площади, ограничиваемой кривой , получаем выражение для

.

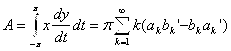Из двух последних равенств вытекает следующее

Отсюда и вытекает изопериметрическое неравенство вместе с единственностью.

Если рассмотреть ту же проблему возле берега моря с прямолинейной границей, то максимальное значение площади получается для полукруга с диаметром на границе. Действительно, пусть некоторая кривая длины Ограничивает береговую область площади . Отразим зеркально кривую и получим кривую , (расположенную в море). Вместе с кривая ограничивают замкнутую плоскую область длины . Применим изопериметрическое неравенство, учитывая, что площадь замкнутой области равна :

. Следовательно, для данного максимальная площадь, ограничиваемая кривой и берегом, равна .

Эта задача носит название задачи Дидоны по имени царицы древней Финикии. Поскольку ее брат, Пигмалион, убил ее мужа и захватил власть, Дидона была вынуждена искать спасения бегством на корабле. Было это в 900 г. до нашей эры. Беглецы высадились на берегу Средиземного моря на месте, где позже был основан Карфаген. Они попросили разрешения у царя Нумидии купить часть территории. Царю не очень понравилась их просьба, но он дипломатично разрешил им купить только ту часть подвластной ему территории, которую может покрыть шкура одного быка. Дидона разрезала шкуру быка на тонкие полоски и связала из них длинную веревку длиной около 1км. Затем она очертила полукруг с диаметром вдоль побережья и выкупила данную территорию площадью около 16 гектаров.

Литература. 1. В. Бляшке, Введение в диф. геометрию, параграфы 24, 29.

< Предыдущая		Следующая >