16. Натуральные уравнения кривой
Мы видели, что если кривизна и кручение кривой в ![]() постоянны, то можно восстановить кривую (винтовую линию ) с данными
постоянны, то можно восстановить кривую (винтовую линию ) с данными ![]() С точностью до движения в пространстве. Оказывается, этот факт справедлив и в общей ситуации, когда кривизна и кручение не являются постоянными.
С точностью до движения в пространстве. Оказывается, этот факт справедлив и в общей ситуации, когда кривизна и кручение не являются постоянными.
Теорема. Пусть ![]() – любые регулярные функции, причем
– любые регулярные функции, причем ![]() . Тогда существует и притом единственная, с точностью до движения в пространстве, кривая, для которой
. Тогда существует и притом единственная, с точностью до движения в пространстве, кривая, для которой ![]() является кривизной, а
является кривизной, а ![]() – кручением в точке, соответствующей дуге
– кручением в точке, соответствующей дуге ![]() .
.
1). Докажем сначала существование кривой. Рассмотрим систему уравнений, которой должны удовлетворять в силу формул Френе векторы касательной ![]() , главной нормали
, главной нормали ![]() , и бинормали
, и бинормали ![]() искомой кривой.
искомой кривой.
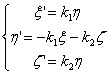 .
.
Пусть ![]() – начальные условия, причем векторы
– начальные условия, причем векторы ![]() образуют ортонормированный правый репер в точке кривой, отвечающей значению
образуют ортонормированный правый репер в точке кривой, отвечающей значению ![]() . Поскольку функции
. Поскольку функции ![]() регулярны, то из общей теории ODE следует, что существует и единственно решение данной системы дифференциальных уравнений первого порядка с данными начальными условиями. Покажем, что решение
регулярны, то из общей теории ODE следует, что существует и единственно решение данной системы дифференциальных уравнений первого порядка с данными начальными условиями. Покажем, что решение ![]() образует ортонормированный правый репер при любом
образует ортонормированный правый репер при любом ![]() . Для этого вычислим
. Для этого вычислим ![]() . Используя уравнения системы Френе, получим
. Используя уравнения системы Френе, получим 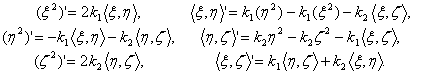
Анализируя эту систему уравнений видим, что она удовлетворяется значениями ![]() С другой стороны, она удовлетворяется значениями
С другой стороны, она удовлетворяется значениями ![]() . Оба решения совпадают при
. Оба решения совпадают при![]() , следовательно, по теореме единственности, решения совпадают тождественно. Кроме того,
, следовательно, по теореме единственности, решения совпадают тождественно. Кроме того, ![]() при всех
при всех ![]() образуют правую тройку, так как детерминант, составленный из них, является непрерывной функцией и может принимать значения
образуют правую тройку, так как детерминант, составленный из них, является непрерывной функцией и может принимать значения ![]() или –1. Но в точке
или –1. Но в точке ![]() он равен
он равен ![]() , следовательно, и при всех
, следовательно, и при всех ![]() он должен быть равен +1.
он должен быть равен +1.
После того, как восстановлен сопровождающий репер Френе искомой кривой, нетрудно восстановить и саму кривую : 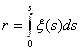 .
.
Проверим, что эта кривая имеет в качестве натуральных уравнений функции ![]() . Во-первых, ясно, что
. Во-первых, ясно, что ![]() является дугой на
является дугой на ![]() , т. к.
, т. к. ![]() Кривизна найденной линии равна
Кривизна найденной линии равна ![]() Кручение равно
Кручение равно
![]()
2). Докажем единственность (с точностью до движения в ![]() ) найденной кривой. Пусть кривые
) найденной кривой. Пусть кривые ![]() и
и ![]() имеют одинаковые натуральные уравнения
имеют одинаковые натуральные уравнения ![]() и их сопровождающие реперы Френе кривых при
и их сопровождающие реперы Френе кривых при ![]() таковы :
таковы : ![]() и
и ![]() . Существует матрица
. Существует матрица ![]() , такая, что
, такая, что ![]() Кроме того, нетрудно проверить, что если
Кроме того, нетрудно проверить, что если ![]() – решение системы уравнений Френе, то
– решение системы уравнений Френе, то ![]() есть другое решение той же системы. В силу единственности решения,
есть другое решение той же системы. В силу единственности решения, ![]()
![]() при всех
при всех ![]() . Интегрируя первое из этих уравнений, получим
. Интегрируя первое из этих уравнений, получим ![]() , где
, где ![]() . Таким образом, кривая
. Таким образом, кривая ![]() получается из
получается из ![]() движением в
движением в ![]() ,ч. т.д.
,ч. т.д.
Литература. А. В. Погорелов. гл. 3, параграф 4.
| < Предыдущая | Следующая > |
|---|