15. Формулы для кривизны и кручения кривой в

Выведем формулы для вычисления кривизны и кручения кривой , заданной в декартовых координатах.

Теорема 1. В каждой точке регулярной кривой класса кривизна определена и неотрицательна. Если – натуральная параметризация, то . Если – произвольная регулярная параметризация, то .

Первое утверждение теоремы следует из уравнения сопровождающего репера Френе, если его возвести в квадрат и воспользоваться тем, что и .

Пусть кривая имеет произвольную регулярную параметризацию Выразим через производные по : , но . Поэтому . Продифференцируем это равенство по : 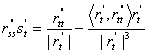и возведем в квадрат. Поскольку и , то 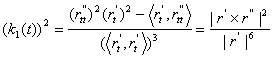, ч. т.д.

Если кривая плоская , то формула для кривизны примет вид . Если плоская кривая задана уравнением , то ее кривизна вычисляется по формуле .

Если на некотором интервале кривизна кривой равна нулю, то в натуральной параметризации и, значит, , где – некоторые постоянные векторы из и кривая представляет собой отрезок прямой в пространстве.

Кривизна допускает следующую геометрическую интерпретацию: пусть и – близкие точки регулярной кривой, обозначим через угол между касательными в этих точках, а через – длину дуги кривой от точки до точки . Тогда кривизна регулярной кривой в точке может быть вычислена по формуле . Действительно, если обозначить единичные касательные векторы в точках через и, то поскольку , то =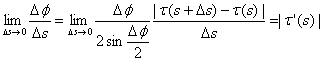

Теорема 2. В каждой точке регулярной класса кривой в , в которой кривизна , определено кручение кривой. Если – натуральная параметризация, то . Если – произвольная параметризация, то .

Если кривая задана в натуральной параметризации, то из последнего уравнения сопровождающего репера Френе находим: 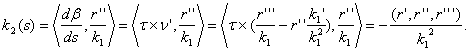Здесь мы воспользовались тем, что, если , то вектор главной нормали и вычислили его производную.

Если теперь кривая взята в произвольной параметризации , то имеем следующие формулы 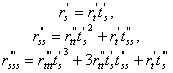. Подставляя их в полученную формулу для кручения (в случае натуральной параметризации) получим, . Воспользуемся, наконец, тем, что и формулой для кривизны в случае произвольной параметризации и получим нужную формулу для кручения.

Покажем, что если кручение некоторой пространственной кривой на интервале равно нулю, то кривая плоская. Действительно, если воспользоваться натуральной параметризацией, то , следовательно, бинормаль . Поскольку , то . Интегрируем и получаем, что , что и означает, что кривая, когда натуральный параметр принадлежит интервалу , находится в плоскости перпендикулярной постоянному вектору .

Две функции (где – дуга некоторой кривой в ) называются натуральными уравнениями кривой. Их задание позволяет найти кривую с точностью до движения в .

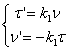Пример. Найдем все кривые в с натуральными уравнениями Возьмем некоторую точку кривой с данными натуральными уравнениями. Можем считать, что точке отвечает значение дуги . Поскольку , то кривая плоская и можно выбрать координаты в так, чтобы бинормаль . Тогда формулы Френе можно записать как дифференциальное уравнение для двумерного вектора : . Поскольку матрица не зависит от , то решение имеет вид . Нетрудно проверить, что 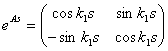. Отсюда получаем, что . Далее интегрируем это уравнение и находим кривую . Если выбрать базис в плоскости следующим образом , то уравнения кривой запишутся в виде . Очевидно, что это есть окружность радиуса .