14. Плоские кривые

Пусть – плоская кривая, параметризованная натуральным параметром ( декартовы координаты). Говорят, что кривая , заданная неявно уравнением имеет соприкосновение порядка с кривой в общей точке если выполнены следующие условий: ,…

.

Условие 0) означает, что кривая пересекается с кривой в точке, отвечающей значению натурального параметра . Условие под номером 1) означает, что в точке пересечения две рассматриваемые кривые имеют общую касательную. Действительно, его можно переписать в виде , что означает перпендикулярность вектора касательной кривой и вектора нормали кривой . Последующие условия говорят о том, что между кривыми есть контакт более высокого порядка, чем первый.

Предложение 1. Если кривизна плоской кривой в точке не равна нулю, то существует единственная окружность, имеющая соприкосновение 2-го порядка с данной кривой в точке Центр соприкасающейся окружности лежит на главной нормали к кривой в точке

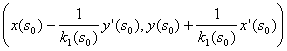, а радиус равен .

Доказательство. Пусть искомая окружность имеет уравнение . Тогда, согласно определению соприкосновения второго порядка, должны выполняться три условия: , ,

Из условия 1) видно, что вектор перпендикулярен вектору касательной. Это значит, что центр соприкасающейся окружности лежит на главной нормали к кривой, т. е. на прямой Из условия 2) можно найти радиус соприкасающейся окружности. Действительно, . По формуле Френе и . Следовательно, , ч. т.д.

Эволютой кривой называется геометрическое место центров кривизны кривой. Если кривая параметризована натуральным параметром , то из предложения 1 следует, что ее эволюта имеет вид

.

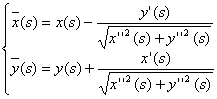В случае произвольной регулярной параметризации кривой уравнение эволюты имеет вид

.

Эвольвентой кривой называется такая кривая , по отношению к которой кривая является эволютой. Выведем уравнения эвольвенты, кривой , параметризованной натуральным параметром . Вектор точки эвольвенты, очевидно, допускает представление . Дифференцируя это равенство по , получим . Отсюда, так как перпендикулярен , имеем . Следовательно, Таким образом, если кривая имеет эвольвенту, то она задается уравнением. Уравнение эвольвенты в случае произвольной параметризации кривой имеет вид

.

Наглядно образование эвольвенты можно себе представить следующим образом. Представим себе нерастяжимую нить, натянутую на часть кривой , соответствующую значениям с концом в точке Если эту нить, оттягивая за конец, сматывать с кривой, то конец нити описывает эвольвенту кривой.

Пусть на плоскости задано семейство кривых , зависящих от параметра . Кривая называется Огибающей семейства , если задана функция (“ правило прикрепления“), удовлетворяющая следующим условиям:, 2) при каждом фиксированном кривая касается кривой , 3) функция непостоянна в любом интервале изменения . Огибающая и произвольная кривая семейства имеют общую нормаль в точке прикрепления.

Примеры. 1) Произвольная регулярная кривая есть огибающая семейства своих касательных. 2) Эволюта кривой есть огибающая семейства ее нормалей.

Предложение 2. Если огибающая семейства кривых существует, то ее уравнение может быть получено из системы уравнений (исключением параметра )

Доказательство. Дифференцируя по условие 1), получим Поскольку каждая кривая семейства касается огибающей, то при любом должно быть выполнено условие: Отсюда получаем, что , ч. т.д.

Литература. 1. А. В. Погорелов, гл.3, параграф 5.

< Предыдущая		Следующая >