13. Метод подвижного репера
Рассмотрим другой способ вывода уравнения Маурера-Картана группы изометрий плоскости ![]() . При этом автоматически получается соответствующее множество левоинвариантных форм. С каждой точкой евклидовой плоскости
. При этом автоматически получается соответствующее множество левоинвариантных форм. С каждой точкой евклидовой плоскости ![]() свяжем ортонормированный репер
свяжем ортонормированный репер ![]() . При этом изменение векторов
. При этом изменение векторов ![]() при переходе в точку
при переходе в точку ![]() описывается уравнениями:
описывается уравнениями:
![]() , (1)
, (1)
Где ![]() – некоторые линейные формы (относительно
– некоторые линейные формы (относительно ![]() ). Действительно, поскольку
). Действительно, поскольку ![]() то
то ![]() и , следовательно,
и , следовательно, ![]() , где
, где ![]() – некоторая пфаффова форма, аналогично можно получить, что
– некоторая пфаффова форма, аналогично можно получить, что ![]() . Остается убедиться, что
. Остается убедиться, что ![]() . Это следует, если продифференцировать уравнение
. Это следует, если продифференцировать уравнение ![]() Проверим, что формы
Проверим, что формы ![]() удовлетворяют уравнениям Маурера-Картана группы Ли
удовлетворяют уравнениям Маурера-Картана группы Ли ![]() . Действительно, если взять внешний дифференциал от первого из уравнений системы (1), то получим
. Действительно, если взять внешний дифференциал от первого из уравнений системы (1), то получим ![]() Подставляя вместо
Подставляя вместо ![]() их выражения из остальных уравнений (1), получим
их выражения из остальных уравнений (1), получим ![]() Отсюда следуют первые два уравнения Маурера-Картана:
Отсюда следуют первые два уравнения Маурера-Картана: ![]() Оставшееся можно получить, дифференцирую внешним образом любое из двух других уравнений системы (1). Например,
Оставшееся можно получить, дифференцирую внешним образом любое из двух других уравнений системы (1). Например, ![]() . Следовательно,
. Следовательно, ![]() Таким образом, проверено, что формы
Таким образом, проверено, что формы ![]() удовлетворяют уравнениям Маурера-Картана группы собственных изометрий плоскости.
удовлетворяют уравнениям Маурера-Картана группы собственных изометрий плоскости.
Уравнения Маурера-Картана подвижного репера евклидова пространства. Поскольку группа ![]() имеет размерность 6, и прямой подсчет структурных констант ее касательной алгебры
имеет размерность 6, и прямой подсчет структурных констант ее касательной алгебры ![]() занимает много времени, мы предпочтем действовать аналогично рассмотренному случаю
занимает много времени, мы предпочтем действовать аналогично рассмотренному случаю ![]() . Изменение подвижного ортонормированного репера
. Изменение подвижного ортонормированного репера ![]() При переходе от точки
При переходе от точки ![]() к точке
к точке![]() описывается уравнениями :
описывается уравнениями : ![]() (2)
(2)
Где ![]() – некоторые пфаффовы формы (от шести переменных). Дифференцируя уравнение
– некоторые пфаффовы формы (от шести переменных). Дифференцируя уравнение ![]() , получим
, получим ![]() (3)
(3)
Поэтому уравнения (2) можно переписать в виде
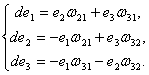 (4)
(4)
Вместе взятые уравнения (4) и первое из уравнений (2) называются Деривационными Уравнениями подвижного репера евклидова пространства ![]() . Однако пфаффовы формы
. Однако пфаффовы формы ![]() должны еще удовлетворять уравнениям Маурера-Картана, которые получаются так же, как и в случае мобильного репера в
должны еще удовлетворять уравнениям Маурера-Картана, которые получаются так же, как и в случае мобильного репера в ![]() . Возьмем внешний дифференциал от первого уравнения системы (2) :
. Возьмем внешний дифференциал от первого уравнения системы (2) : ![]()
![]() Отсюда следуют первые три уравнения Маурера-Картана:
Отсюда следуют первые три уравнения Маурера-Картана:
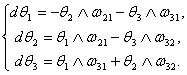 (5)
(5)
Аналогично, взяв внешний дифференциал от первого из уравнений (4) , получим ![]()
![]()
Если таким же образом поступить с другим уравнением из (4), то получим оставшиеся три уравнения Маурера-Картана подвижного репера в ![]()
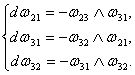 (6)
(6)
Можно показать, что выполнение уравнений (5), (6) является достаточным условием для интегрируемости уравнений (4), (2).
Инварианты гладкой кривой в ![]() . Рассмотрим гладкую кривую
. Рассмотрим гладкую кривую ![]() в
в ![]() , параметризованную натуральным параметром
, параметризованную натуральным параметром ![]() . Существует удобный способ выбрать сопровождающий репер кривой следующим образом : расположим вектор
. Существует удобный способ выбрать сопровождающий репер кривой следующим образом : расположим вектор ![]() вдоль касательной к кривой в точке
вдоль касательной к кривой в точке ![]() , т. е.
, т. е. ![]() . Следовательно, при таком выборе пфаффовы формы
. Следовательно, при таком выборе пфаффовы формы ![]() , Затем расположим вектор
, Затем расположим вектор ![]() вдоль бесконечно малого вектора
вдоль бесконечно малого вектора ![]() . Тогда
. Тогда ![]() , поскольку всегда выполнено уравнение
, поскольку всегда выполнено уравнение ![]() .
.
Идея адаптировать таким образом подвижный репер к гладкой кривой восходит к F. Frenet (1847) и поэтому он и носит название подвижного репера Френе. Деривационные уравнения сопровождающего репера Френе выглядят следующим образом: 
В классической дифференциальной геометрии за векторами ![]() репера Френе закрепились названия:
репера Френе закрепились названия: ![]() – Вектор касательной,
– Вектор касательной, ![]() – Вектор главной нормали, вектор
– Вектор главной нормали, вектор ![]() носит название Бинормали. Функция
носит название Бинормали. Функция ![]() называется Кривизной Кривой
называется Кривизной Кривой ![]() в
в ![]() , функция
, функция ![]() называется Кручением кривой. Следовательно, в классической дифференциальной геометрии уравнения сопровождающего репера Френе имеют вид
называется Кручением кривой. Следовательно, в классической дифференциальной геометрии уравнения сопровождающего репера Френе имеют вид 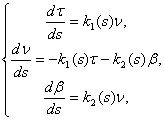 где
где ![]()
![]() – натуральный параметр кривой
– натуральный параметр кривой ![]() . Функции
. Функции ![]() являются инвариантами кривой в
являются инвариантами кривой в ![]() .
.
Литература. 1.В. Бляшке, Введение в диф. геометрию, параграфы 21– 24.
2. Ж. Фавар, Курс локальной диф. геометрии. Часть 2. Гл. 1.
| < Предыдущая | Следующая > |
|---|