12. Структурные константы и уравнения Маурера-Картана

Пусть – некоторый базис в касательной алгебре Ли . Тогда для скобки двух базисных векторов (и соответствующих им левоинвариантных полей) имеем разложение Величины называются Структурными константами алгебры Ли . Они зависят от выбора базиса в и являются компонентами тензора ранга . Кроме того, поскольку скобка антикоммутативна, то 1), и поскольку имеет место тождество Якоби, то 2). Обратно, если задан тензор ранга , удовлетворяющий условиям 1)-2) , то продолжив определение скобки по линейности, получим и тем самым определим структуру алгебры Ли на

Базисным левоинвариантным векторным полям на группе Ли соответствует двойственный базис Сопряженного пространства, определяемый равенствами . Линейные формы образуют базис Левоинвариантных форм на группе , для которых выполняется условие при любом . В частности, формы Линейно независимы в каждой точке , а, значит, и форма Однозначно определена на и не обращается в нуль. Отсюда вытекает, что всякая группа Ли есть ориентируемое многообразие.

Пример. Алгебра Ли группы натянута на следующие векторы: 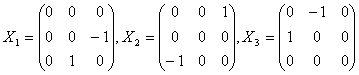. Непосредственный подсчет дает:Следовательно, изоморфна классической алгебре Ли векторов в , в которой скобка двух векторов есть их векторное произведение: .

Теорема. Для левоинвариантных форм на группе Ли справедливы уравнения Маурера-Картана: ,

где – структурные константы алгебры Ли , соответствующие двойственному базису .

Доказательство. Поскольку формы левоинвариантны, то . Применяя оператор антиувлечения к обеим частям равенства, получим, что , т. е. в разложении по базису функции есть константы. Остается проверить, что они совпадают с . Для этого применим формулу для . Получим С другой стороны, правая часть равна , ч. т.д.

Пример. Рассмотрим группу собственных изометрий евклидовой плоскости. Как известно, она может быть представлена как матричная подгруппа вида 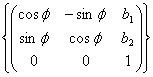группы . Касательная алгебра состоит из векторов вида 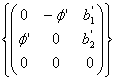, Мы можем в качестве базисных векторов выбрать : 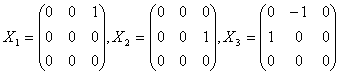. Вычисления скобок базисных векторов дают Следовательно, ненулевые структурные константы таковы: Обозначим двойственные левоинвариантные формы в данном примере следующим образом : . Тогда уравнения Маурера-Картана для группы Ли примут вид:

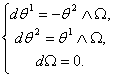
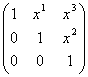Пример. Левоинвариантная метрика на группе . На примере группы Гейзенберга третьего порядка покажем, как вводится левоинвариантная метрика на группе Ли. Отождествим многообразие с пространством так, что матрица соответствует точке . Тогда групповой закон умножения в может быть записан в виде

Легко вычислить, что дифференциал левого сдвига равен

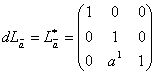. Пусть метрический тензор на группе в единице (т. е. в касательном пространстве в точке ) совпадает с тензором Кронекера, т. е. равен . Поскольку метрический тензор представляет собой ковариантный тензор, то при левом сдвиге он сносится с образа на прообраз, т. е. с касательного пространства на касательное пространство , где он нами задан. Значит, . Обратным отображение к является , матрица Якоби для которого является обратной к . Следовательно, она равна 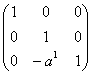Поэтому, для нахождения коэффициентов метрического тензора в точке получаем формулу. Напомним, что по формуле из лекции 3 ковариантный метрический тензор при антиувлечении вычисляется по формуле . Значит, получаются следующие выражения для метрического тензора на в точке : , , . Иначе говоря, левоинвариантная метрическая форма в точке может быть записана в виде , который приведен в книге П. Скотта “ Геометрии на трехмерных многообразиях” на с.123.

В заключение приведем классификацию алгебр Ли размерности 1 и 2.

1-Мерные алгебры Ли. Ясно, что с точностью до изоморфизма существует только одна действительная алгебра Ли размерности 1, именно с нулевой скобкой. Она является касательной алгеброй различных связных групп Ли : и .

2-мерные алгебры Ли. Пусть есть двумерная алгебра Ли с базисными элементами . Тогда вся структура алгебры Ли определяется скобкой на базисных элементах Если то все скобки равны нулю и алгебра абелева. Если хотя бы одно из чисел ненулевое, можно считать, что . Тогда, рассматривая новый базис и , мы получим . Поскольку тождество Якоби справедливо для таким образом определенной скобки Ли, это действительно двумерная алгебра Ли. Таким образом, с точностью до изоморфизма существует только две различных 2-мерных алгебры Ли.

Абелева алгебра является касательной алгеброй для . Примером группы Ли с неабелевой двумерной алгеброй является матричная группа вида 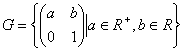. Можно показать, что это единственная ( с точностью до изоморфизма) связная неабелева группа Ли размерности 2.

Литература. 1. Дубровин Б. А, и др. Современная геометрия, параграф 21,

2. С. Стернберг, гл.5, параграф 2. 3. Зуланке Р. Винтген П.

Дифференциальна геометрия и расслоения, гл.1 параграф 10.

4. R. Bryant, An introduction to Lie Groups and Symplectic Geometry.

Lecture 2, in “Geometry and Quantum Field Theory”, 1995.

< Предыдущая		Следующая >