10. Производная Ли

Тензорные поля и дифференциальные формы можно дифференцировать вдоль векторного поля. Соответствующий оператор называется производной Ли.

Определим производную Ли векторного поля вдоль векторного поля. Проследим интегральную кривую поля , проходящую через точку до точки и возьмем вектор поля . Затем подействуем на него дифференциалом локального диффеоморфизма . При этом получается вектор, принадлежащий касательному пространству . Найдем разность векторов , разделим ее на и перейдем к пределу при . В итоге мы получаем вектор из касательного пространства , который и называется Производной Ли поля вдоль поля в точке , и который обозначается . Следовательно, (3)

Аналогично определяется Производная Ли дифференциальной формы вдоль векторного поля с той лишь разницей, что значение формы в точке сносится в точку при помощи отображения . Затем рассматриваем его разность с , делим на и переходим к пределу при . Следовательно,

(4)

Определим Производную Ли произвольного тензорного поля вдоль векторного поля следующим образом:

Можно показать, что выше данные определения производных Ли векторного поля и дифференциальной формы совпадают с этим общим определением производной Ли тензорного поля. Следующее предложение позволяет производить конкретные вычисления производных Ли наиболее важных геометрических объектов.

Предложение 1. Пусть – гладкое векторное поле. Тогда

для любой гладкой функции На многообразии,

для произвольного векторного поля На многообразии,

– для любой дифференциальной формы на .

Доказательство. Функция представляет собой тензор нулевого ранга, т. е. скаляр. Потому, согласно общей формуле Получилась формула для производной функции по направлению вдоль векторного поля .

Пусть тензор типа (1,0), т. е. векторное поле . Согласно общей формуле имеем:

Пусть тензорное поле имеет ранг (0,1), т. е. представляет собой дифференциальную 1-форму . Согласно общей формуле : , ч. т.д.

Предложение 2. Для любого векторного поля и дифференциальной формы справедливо равенство:

Для произвольной 1-формы и векторного поля Справедливы равенства

Доказательство. Поскольку производная Ли дифференциальной формы получается при помощи операции антиувлечения , которая коммутирует с операцией взятия внешнего дифференциала , то взятие производной Ли от формы коммутирует с .

Пусть . Пусть , . Тогда , и . С другой стороны, , поэтому 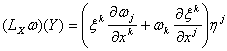. Также имеем , откуда и следует справедливость .

Определим выражение , где – некоторая дифференциальная форма степени , а – векторные поля. Пусть, сначала , где все – формы степени 1. Тогда положим . Если есть произвольная -форма, то ее можно представить в виде суммы простых форм рассмотренного вида и по линейности определить выражение . Предположим, что (для простоты) и , а . Тогда получим , Далее . Наконец,