07. Скобка векторных полей на многообразии

Пусть на многообразии заданы два векторных поля в окрестности точки : .

Лемма. Пусть и – дифференцируемые векторные поля на многообразии . Тогда существует единственное векторное поле такое, что для всякой функции справедливо равенство .

Доказательство. Вычислим действие оператора на функцию : 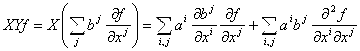. Аналогично можно получить выражение для . Вычитая их приходим к равенству . Таким образом, коэффициенты поля определены однозначно в данной карте . Непосредственно проверяется их тензорный закон преобразования при переходе к другой локальной карте .

Векторное поле , полученное в лемме, называется Скобкой векторных полей и . Операция взятия скобки обладает следующими свойствами.

Предложение. Если – дифференцируемые векторные поля на многообразии , – действительные числа, и – дифференцируемые функции на , то

(антикоммутативность),

(линейность),

(тождество Якоби),

.

Доказательство. Первые два свойства следуют из определения скобки. Докажем :. Циклической перестановкой получаем два остальных слагаемых. Затем убеждаемся, что сумма всех трех выражений равна нулю. Докажем : =

В дифференциальной геометрии часто используется следующая теорема Фробениуса о полной интегрируемости распределения -мерных плоскостей в касательном расслоении. Полная интегрируемость означает существование семейства -мерных поверхностей, касательные плоскости к которым совпадают с заданным распределением ( доказательство имеется, например, в книге С. Стернберга, с.144.).

Теорема. Пусть векторные поля , заданные на многообразии , порождают некоторое распределение -мерных плоскостей в касательном расслоении над . Данное распределение является вполне интегрируемым тогда и только тогда, когда существуют такие функции на многообразии, что .

Пример. Рассмотрим распределение двумерных плоскостей в , натянутое на векторные поля и . Вычислим скобку Ли векторных полей .

Имеем 1) 2) , 3) . Следовательно, (там, где . Поэтому распределение двумерных плоскостей в , натянутых на , является интегрируемым. Действительно, легко проверить, что семейство сфер касается данного распределения.

< Предыдущая		Следующая >