06. Объем ориентированного риманова многообразия

Пусть в окрестности точки риманова многообразия задана карта и векторные поля такие, что Выберем в ортонормированный базис , в котором значения векторного поля в точке можно записать в виде: . Тогда Поскольку объем Параллелепипеда, построенного на векторах в касательном пространстве равен , то мы имеем (поскольку ). Если – какая-то другая карта в окрестности точки , имеющая согласованную ориентацию с картой , то в этой карте базисные поля имеют вид и коэффициенты метрического тензора равны и , где 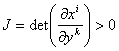(якобиан матрицы Якоби замены координат).

Теперь можно определить понятие объема области ориентированного риманова многообразия . Пусть на римановом многообразии с метрическим тензором дана область , замыкание которой компактно, граница гладкая и существует ориентируемая окрестность множества . Объемом области называется число . Легко проверить, что значение данного интеграла не зависит от выбора локальной системы координат.

Пример. Рассмотрим погруженную поверхность 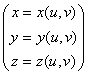В . В этом случае можно говорить о Площади () области на поверхности. Коэффициенты метрического тензора при этом равны , следовательно, всякая область с компактным замыканием на поверхности имеет площадь: .

< Предыдущая		Следующая >