05. Метрическая форма погруженного многообразия и изометрии

Пусть риманово многообразие с метрическим тензором и рассмотрим погружение Многообразия в . Если карта на , а – карта на , то погружение можно определить следующим образом : . Тогда говорят, что на определена Риманова метрика антиувлечения билинейной формы , где . Именно, если векторы с помощью дифференциала отображаются в , то . Поскольку при погружении ненулевой вектор переходит в ненулевой, то квадратичная форма положительно определенная и симметрическая. Коэффициенты этой метрики можно найти по формуле:

где .

Пример. Рассмотрим погружение области с координатами в евклидово пространство : 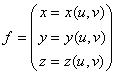. Поскольку метрический тензор равен , то на

Погруженной поверхности возникает метрический тензор (индуцированный погружением) с коэффициентами . Согласно общей формуле : ,

Где через обозначен вектор-столбец производных отображения . Аналогично, , .

В классической дифференциальной геометрии со времен К. Ф. Гаусса используются обозначения Метрический тензор поверхности также называют Первой фундаментальной формой и, если вектор касательного пространства имеет координаты , то квадрат его длины равен .

Пусть задано погружение риманова многообразия в другое риманово многообразие . Если в окрестности некоторой точки метрический тензор совпадает с тензором , то говорят, что погружение Является Локальной изометрией.

Если отображение является диффеоморфизмом, то оно называется Изометрией риманова Многообразия на риманово многообразие .

Пример. Рассмотрим отображение плоскости с декартовыми координатами в евклидово пространство в виде цилиндра: . Легко вычислить, что коэффициенты первой фундаментальной формы погружения (цилиндра) равны : , , т. е. метрика, индуцированная погружением, совпадает со стандартной на . Следовательно, цилиндр локально изометричен плоскости. Однако это отображение не является глобальной изометрией, поскольку у цилиндра и плоскости имеются топологические различия.

В классической дифференциальной геометрии поверхности и называют Изометричными, если существует взаимно однозначное отображение поверхностей, при котором соответствующие кривые на этих поверхностях имеют одинаковые длины.

Теорема. Если гладкие поверхности и можно параметризовать так, что их первые фундаментальные формы будут одинаковы, то поверхности изометричны. Изометрическое отображение заключается в сопоставлении точек с одинаковыми координатами. Обратно, если поверхности и изометричны, то они могут быть параметризованы так, что их первые фундаментальные формы будут одинаковы.

Доказательство.1) Если кривая задается уравнениями , то соответствующая ей кривая На поверхности имеет те же уравнения и поскольку длина кривой вычисляется по формуле 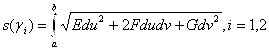, то .

2) Пусть между поверхностями установлено взаимно однозначное соответствие, при котором длины соответствующих кривых равны (изометрия). Можно показать, что оба параметрических уравнения поверхностей : и задаются гладкими функциями, имеющими общую область определения . Покажем, что в такой параметризации коэффициенты первых фундаментальных форм поверхностей и равны. Рассмотрим сначала кривые на поверхностях и . Их длины равны по предположению об изометрии, следовательно . Так как это равенство справедливо при любом , то подынтегральные функции равны, следовательно . Аналогично, рассматривая координатные кривые , можно получить, что . Наконец, рассматривая изометрию кривых можно получить равенство коэффициентов .

Если изометрия действует из в себя, то она также называется Движением риманова пространства . Движения любого риманова многообразия образуют группу .

Предложение. Группа движений евклидова пространства с метрикой изоморфна матричной группе , где .

Доказательство. Из курса аналитической геометрии известно, что произвольное движение пространства имеет вид

. Определим изоморфизм группы в указанную матричную группу следующим образом .

. Остается проверить, что композиции двух изометрий отвечает следующая матрица в группе : .

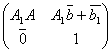Плоскостью Лобачевского Называется верхняя полуплоскость с метрикой .

Предложение. Если , то любое преобразование вида – движение плоскости Лобачевского.

Доказательство. Прямым вычислением можно установить, что 1) , и что 2) верхняя полуплоскость переходит при данном преобразовании в себя. Следовательно, длины кривой и кривой равны в указанной метрике .

Матрицы вида образуют группу (special linear Group) . Поэтому можно сказать, что группа дробно линейных преобразований плоскости содержится в группе .

Литература. 1.В. В. Трофимов. Гл.1, параграф 15,

2. А. В. Погорелов. гл. 6, параграфы 1, 2, 5.

< Предыдущая		Следующая >