04. Элементы римановой геометрии

Связное многообразие называется Римановым, если в нем задано тензорное поле такое, что а) , б) квадратичная форма с коэффициентами положительно определена. Тензор типа (0,2) называется Метрическим тензором.

В каждом касательном пространстве к многообразию возникает евклидова геометрия со скалярным произведением векторов .

Определим Контравариантный метрический тензор : .

Пример. Рассмотрим евклидову плоскость с декартовыми координатами . Она является римановым многообразием, поскольку метрический тензор равен – тензор Кронекера. При переходе к полярным координатам компоненты метрического тензора должны преобразоваться согласно закону преобразования тензора типа (0,2): , (где имеется в виду, что). Поэтому в полярных координатах метрика евклидовой плоскости имеет вид 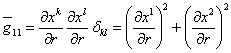, 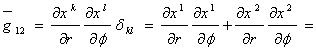0, .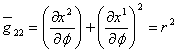

В римановом многообразии верхние и нижние индексы тензора можно опускать и поднимать с помощью свертки его с метрическим тензором. Например, вектору отвечает Двойственный ковектор , а произвольному ковектору соответствует двойственный вектор . Аналогичным образом поднимают и опускают индексы для тензора любого вида. Если метрика пространства в данной точке есть , то, очевидно, нет различия между компонентами вектора и двойственного ему ковектора, т. к. .

Пусть в римановом многообразии задана кривая . Длиной этой кривой называется число 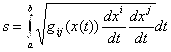. Это определение корректно, т. е. оно не зависит от выбора системы координат и от выбора параметра на кривой.

Примеры. 1) Вычислим длину винтовой линии 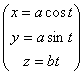в евклидовом пространстве. Поскольку метрический тензор в декартовых координатах совпадает с тензором Кронекера, то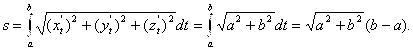

Заметим, что формулу для длины кривой можно представить в следующем виде: , где – касательный вектор к кривой в точке .

2) Рассмотрим кривую 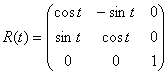в группе . Прежде чем вычислять ее длину, укажем, что группа является подгруппой группы невырожденных матриц третьего порядка . Группу можно рассматривать, как подмножество девятимерного евклидова пространства , причем каждая матрица имеет длину . Касательным вектором для кривой в точке будет матрица . Вычисления дают длину этого вектора . Следовательно, длина рассматриваемой кривой (гомеоморфной окружности) будет .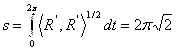

Длину кривой можно выбрать в качестве нового параметра, тогда длина касательного вектора к ней в любой точке будет равна 1. Такой параметр называется Натуральным.

Пусть на римановом многообразии в точке пересекаются две кривые : и . Углом между данными кривыми называется угол между их касательными векторами и в касательном пространстве . Для его нахождения используют формулу

.

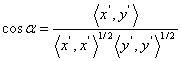Пример 1. Найдем на сфере линии, которые пересекают меридианы под постоянным углом (Локсодромы). Поскольку в географических координатах сфера имеет параметризацию 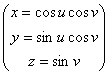, , то мы можем искать линию в виде . Касательный вектор к ней есть 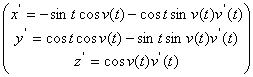. Длина его равна . Меридиан имеет уравнения . Касательный вектор к меридиану есть 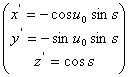, длина его равна 1. Пусть две кривые пересекаются в точке . Скалярное произведение касательных векторов к меридиану и локсодроме равно . По формуле угла между кривыми получаем . Отсюда получается уравнение . Интегрируя его, находим решение

Пример 2. Покажем, что логарифмическая спираль, заданная в полярных координатах уравнением пересекает все лучи, выходящие из полюса под постоянным углом. Действительно, в полярных координатах данная спираль может быть записана так 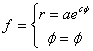. Касательный вектор к ней есть 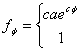. Касательный вектор к радиальному лучу 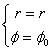имеет вид . Используем вид метрического тензора в полярных координатах и получим по формуле угла между кривыми .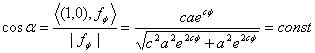

Литература.1. Трофимов гл 1, параграфы 11, 15.

2. О. А. Борисенко гл.1, 1.5.,

< Предыдущая		Следующая >