94. Свойства функций, непрерывных на отрезке
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т. е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т. е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
M £ f(x) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется Колебанием Функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т. е. если sign(f(a)) ¹ sign(f(b)), то $ х0: f(x0) = 0.
Определение. Функция f(x) называется Равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х1Î[a, b] и x2Î[a, b] таких, что
ïх2 – х1ï< D
Верно неравенство ïf(x2) – f(x1)ï < e
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример. ![]()
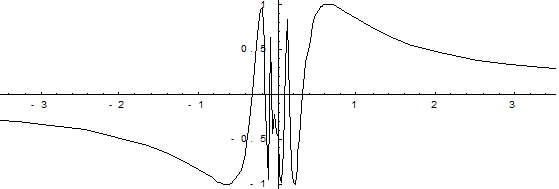
Функция ![]() непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т. к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т. к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
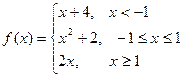
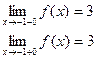
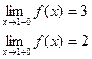
В точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
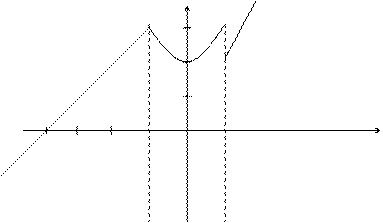 у
у
3
2
-4 -1 0 1 х
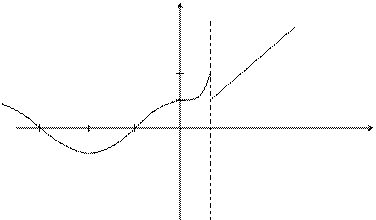
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
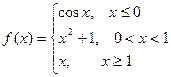
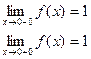
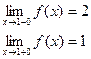
В точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
 |
у
2
1
- p - p/2 0 1 x
| < Предыдущая | Следующая > |
|---|