89. Непрерывность функции в точке

Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется Непрерывной в точке Х0, если предел функции и ее значение в этой точке равны, т. е.

Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется Разрывной функцией, а точка х0 – точкой разрыва.

Пример непрерывной функции:

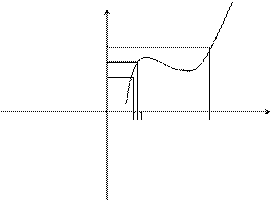y

f(x0)+e

f(x0)

f(x0)-e

0 x0-D x0 x0+D x

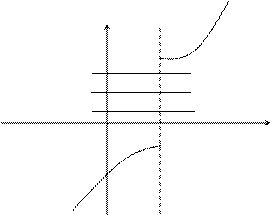Пример разрывной функции:

y

f(x0)+e

f(x0)

f(x0)-e

x0 x

Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

Верно неравенство .

Определение. Функция f(x) называется Непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.

F(x) = f(x0) + a(x)

Где a(х) – бесконечно малая при х®х0.

< Предыдущая		Следующая >