88. Некоторые замечательные пределы

Первый замечательный предел. , где P(x) = a0xn + a1xn-1 +…+an,

Q(x) = b0xm + b1xm-1 +…+bm - многочлены.

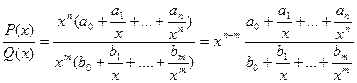
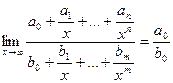
Итого: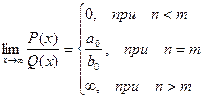

Второй замечательный предел.

Третий замечательный предел.

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

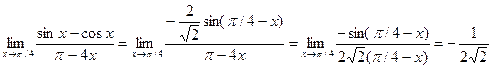
Пример. Найти предел.

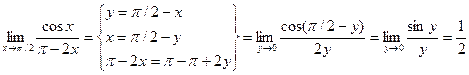
Пример. Найти предел.

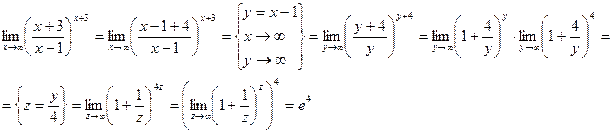
Пример. Найти предел .

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

X2 – 6X + 8 = 0; X2 – 8X + 12 = 0;

D = 36 – 32 = 4; D = 64 – 48 = 16;

X1 = (6 + 2)/2 = 4; X1 = (8 + 4)/2 = 6;

X2 = (6 – 2)/2 = 2 ; X2 = (8 – 4)/2 = 2;

Тогда

Пример. Найти предел.

домножим числитель и знаменатель дроби на сопряженное выражение: =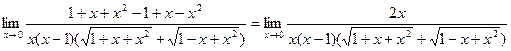

=.

Пример. Найти предел.

Пример. Найти предел .

Разложим числитель и знаменатель на множители.

X2 – 3X + 2 = (X – 1)(X – 2)

X3 – 6X2 + 11X – 6 = (X – 1)(X – 2)(X – 3), т. к.

X3 – 6x2 + 11x – 6 x - 1

x3 – x2 x2 – 5x + 6

- 5x2 + 11x

- 5x2 + 5x

6x - 6

6x - 6 0

X2 – 5x + 6 = (x – 2)(x – 3)

Тогда

Пример. Найти предел.

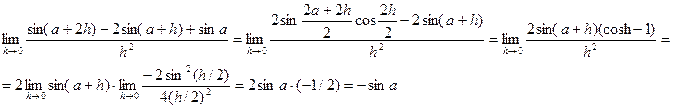
Для самостоятельного решения:

1)

2)

3)

4)

5)

6)

7)

8) - не определен.

< Предыдущая		Следующая >