73. Матрицы линейных преобразований

Пусть в n - мерном линейном пространстве с базисом ,,…, задано линейное преобразование А. Тогда векторы А,А,…,А- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

A= a11+ a21+…+ an1

A= a12+ a22+…+ an2

……………………………….

A= an1+ an2+…+ ann

Тогда матрица А = называется Матрицей линейного преобразования А.

Если в пространстве L взять вектор = x1+ x2+…+ xn, то AÎ L.

, где

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе ,,…,.

В матричном виде:

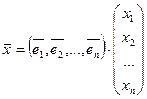, А×,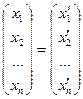

Пример. Найти матрицу линейного преобразования, заданного в виде:

X¢ = x + y

Y¢ = y + z

Z¢ = z + x

X¢ = 1×x + 1×y + 0×z

Y¢ = 0×x + 1×y + 1×z

Z¢ = 1×x + 0×y + 1×z

A =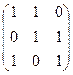

На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.

Определение: Если вектор Переводится в вектор линейным преобразованием с матрицей А, а вектор в вектор линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор в вектор (оно называется Произведением составляющих преобразований).

С = В×А

Пример. Задано линейное преобразование А, переводящее вектор В вектор и линейное преобразование В, переводящее вектор в вектор . Найти матрицу линейного преобразования, переводящего вектор в вектор .

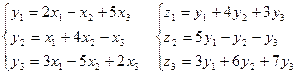
С = В×А

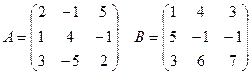
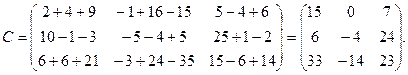
Т. е.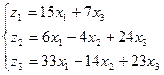

Примечание: Если ïАï= 0, то преобразование вырожденное, т. е., например, плоскость преобразуется не в целую плоскость, а в прямую.

< Предыдущая		Следующая >