66. Поверхности вращения

Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется Поверхностью вращения С осью вращения d.

Если уравнение поверхности в прямоугольной системе координат имеет вид:

F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.

Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,

F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.

Запишем уравнения поверхностей вращения для некоторых частных случаев:

1) - Эллипсоид вращения

2) - Однополостный гиперболоид вращения

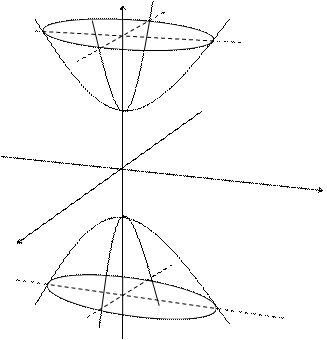
3) - Двуполостный гиперболоид вращения

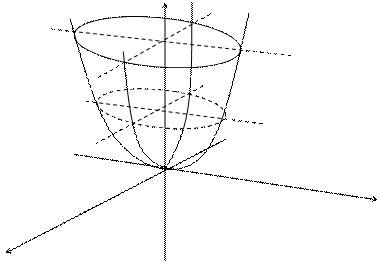
4) - Параболоид вращения

Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу.

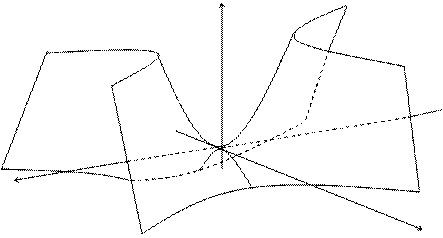
Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:

Сфера:

Трехосный эллипсоид:

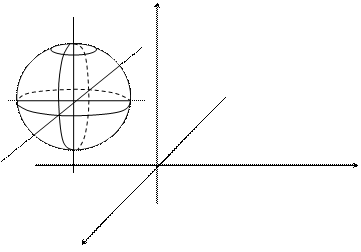В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.

Однополостный гиперболоид:

Двуполостный гиперболоид:

Эллиптический параболоид:

Гиперболический параболоид:

Конус второго порядка:

< Предыдущая		Следующая >