14. Решение произвольных систем линейных уравнений

Как было сказано выше, Матричный метод и Метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений.

Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:

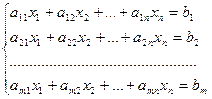, (1)

Где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется Совместной. Если система не имеет ни одного решения, то она называется Несовместной.

Определение. Система называется Определенной, если она имеет только одно решение и Неопределенной, если более одного.

Определение. Для системы линейных уравнений вида (1) матрица

А = 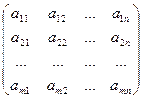называется матрицей системы, а матрица

А*= 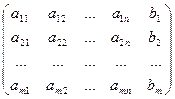называется расширенной матрицей системы

Определение. Если b1, b2, …,bm = 0, то система называется Однородной. однородная система всегда совместна.

< Предыдущая		Следующая >