13. Теорема. (Правило Крамера)
Теорема. Система из N уравнений с N неизвестными

В случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
Xi = DI/D, где
D = Det A, а DI – определитель матрицы, получаемой из матрицы системы заменой столбца I Столбцом свободных членов Bi.
DI = 
Пример.
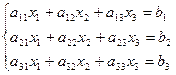
A =  ; D1=
; D1= 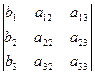 ; D2=
; D2=  ; D3=
; D3= 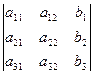 ;
;
X1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:

D =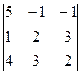 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 =  = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
X1 = D1/D = 1;
D2 =  = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
X2 = D2/D = 2;
D3 = 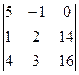 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
X3 = D3/D = 3.
Как видно, результат совпадает с результатом, полученным Выше матричным методом.
Если система однородна, т. е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
При D = 0 система имеет бесконечное множество решений.
Для самостоятельного решения:
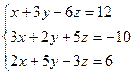 ; Ответ: X = 0; Y = 0; Z = -2.
; Ответ: X = 0; Y = 0; Z = -2.
| < Предыдущая | Следующая > |
|---|