07. Обратная матрица

Определим операцию деления матриц как операцию, обратную умножению.

Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию:

XA = AX = E,

Где Е - единичная матрица того же самого порядка, то матрица Х называется Обратной К матрице А и обозначается А-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Рассмотрим общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E Þ , i=(1,n), j=(1,n),

Eij = 0, i ¹ j,

Eij = 1, i = j.

Таким образом, получаем систему уравнений:

,

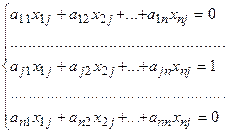Решив эту систему, находим элементы матрицы Х.

Пример. Дана матрица А = , найти А-1.

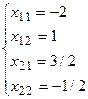
Таким образом, А-1=.

Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

,

Где Мji- Дополнительный минор элемента Аji матрицы А.

Пример. Дана матрица А = , найти А-1.

Det A = 4 - 6 = -2.

M11=4; M12= 3; M21= 2; M22=1

x11= -2; x12= 1; x21= 3/2; x22= -1/2

Таким образом, А-1=.

< Предыдущая		Следующая >