53. Ряды Фурье
( Жан Батист Жозеф Фурье (1768 – 1830) – французский математик)
Определение. Тригонометрическим рядом Называется ряд вида:
![]()
Или, короче, ![]()
Действительные числа Ai, Bi называются коэффициентами тригонометрического ряда.
Если ряд представленного выше типа сходится, то его сумма представляет собой периодическую функцию с периодом 2p, т. к. функции sinNx и cosNx также периодические функции с периодом 2p.
Пусть тригонометрический ряд равномерно сходится на отрезке [-p; p], а следовательно, и на любом отрезке в силу периодичности, и его сумма равна F(X).
Определим коэффициенты этого ряда.
Для решения этой задачи воспользуемся следующими равенствами:
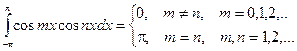
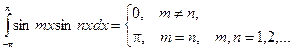
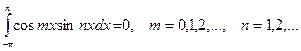
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул. Подробнее см. Интегрирование тригонометрических функций.
Т. к. функция F(X) непрерывна на отрезке [-p; p], то существует интеграл

Такой результат получается в результате того, что  .
.
Получаем: 
Далее умножаем выражение разложения функции в ряд на cosNx и интегрируем в пределах от - p до p.
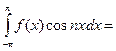

Отсюда получаем: 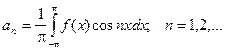
Аналогично умножаем выражение разложения функции в ряд на sinNx и интегрируем в пределах от - p до p.
Получаем: 
Выражение для коэффициента А0 является частным случаем для выражения коэффициентов An.
Таким образом, если функция F(X) – любая периодическая функция периода 2p, непрерывная на отрезке [-p; p] или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты
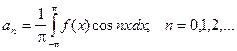

Существуют и называются Коэффициентами Фурье Для функции F(X).
Определение. Рядом Фурье Для функции F(X) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции F(X) сходится к ней во всех ее точках непрерывности, то говорят, что функция F(X) разлагается в ряд Фурье.
| < Предыдущая | Следующая > |
|---|