52. Решение дифференциальных уравнений с помощью сТепенных рядов

С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

Рассмотрим линейное дифференциальное уравнение вида:

Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

Это решение можно представить степенным рядом:

Для нахождения решения остается определить неизвестные постоянные Ci.

Эта задача решается Методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

Затем приравниваем коэффициенты при одинаковых степенях Х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты Ci.

Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.

Пример. Найти решение уравнения C начальными условиями Y(0)=1, Y’(0)=0.

Решение уравнения будем искать в виде

Подставляем полученные выражения в исходное уравнение:

Отсюда получаем:

………………

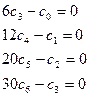
Получаем, подставив начальные условия в выражения для искомой функции и ее первой производной:

Окончательно получим:

Итого:

Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название Метод последовательного дифференцирования.

Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

Если заданные начальные условия Y(0)=1, Y’(0)=0 подставить в исходное дифференциальное уравнение, получим, что

Далее запишем дифференциальное уравнение в виде и будем последовательно дифференцировать его по Х.

После подстановки полученных значений получаем:

< Предыдущая		Следующая >