29. Векторная функция скалярного аргумента

z

A(x, y, z)

y

х

Пусть некоторая кривая в пространстве задана параметрически:

X = j(t); y = y(t); z = f(t);

Радиус - вектор произвольной точки кривой: .

Таким образом, радиус - вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора .

Запишем соотношения для некоторой точки t0:

Тогда вектор - предел функции (t). .

Очевидно, что

, тогда

.

Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус - вектора при некотором приращении параметра t.

; ;

Или, если существуют производные j¢(t), y¢(t), f¢(t), то

Это выражение – вектор производная вектора .

Если имеется уравнение кривой:

X = j(t); y = y(t); z = f(t);

То в произвольной точке кривой А(xА, yА, zА) с радиус - вектором

Можно провести прямую с уравнением

Т. к. производная - вектор, направленный по касательной к кривой, то

.

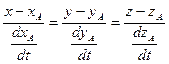< Предыдущая		Следующая >