28. Схема исследования функций

Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:

1) Область существования функции.

Это понятие включает в себя и область значений и область определения функции.

2) Точки разрыва. (Если они имеются).

3) Интервалы возрастания и убывания.

4) Точки максимума и минимума.

5) Максимальное и минимальное значение функции на ее области определения.

6) Области выпуклости и вогнутости.

7) Точки перегиба.(Если они имеются).

8) Асимптоты.(Если они имеются).

9) Построение графика.

Применение этой схемы рассмотрим на примере.

Пример. Исследовать функцию И построить ее график.

Находим область существования функции. Очевидно, что Областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).

В свою очередь, видно, что прямые х = 1, х = -1 являются Вертикальными асимптотами кривой.

Областью значений Данной функции является интервал (-¥; ¥).

Точками разрыва функции являются точки х = 1, х = -1.

Находим Критические точки.

Найдем производную функции

Критические точки: x = 0; x = -; x = ; x = -1; x = 1.

Найдем вторую производную функции

.

Определим выпуклость и вогнутость кривой на промежутках.

-¥ < x < -, y¢¢ < 0, кривая выпуклая

- < x < -1, y¢¢ < 0, кривая выпуклая

-1 < x < 0, y¢¢ > 0, кривая вогнутая

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < , y¢¢ > 0, кривая вогнутая

< x < ¥, y¢¢ > 0, кривая вогнутая

Находим промежутки Возрастания И Убывания функции. Для этого определяем знаки производной функции на промежутках.

-¥ < x < -, y¢ > 0, функция возрастает

- < x < -1, y¢ < 0, функция убывает

-1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢¢ > 0, функция возрастает

Видно, что точка х = - является точкой Максимума, а точка х = является точкой Минимума. Значения функции в этих точках равны соответственно 3/2 и -3/2.

Про вертикальные Асимптоты было уже сказано выше. Теперь найдем Наклонные асимптоты.

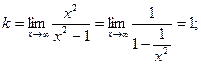
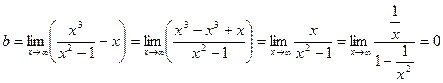
Итого, уравнение наклонной асимптоты – y = x.

Построим График функции:

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая проводит полное исследование функций по приведенной выше схеме. Достаточно ввести функцию, программа выведет подробный отчет о результатах исследования по каждому пункту.

Для запуска программы дважды щелкните по значку:

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

< Предыдущая		Следующая >