53. Коэфициент корреляции

Рассмотрим случай вычисления теоретического корреляционного соотношения , когда связь между случайными величинами Х и Y является Линейной.

Такая форма связи между Х и Y имеет место в случае, когда случайные величины подчиняются двуменому нормальному закону распределения.

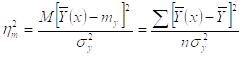
Подставив вместо Y и Их значения для случая линейной зависимости:

=

(х)=а0 + а1х

=

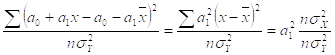
Заменим а1 ее значением, полученным из решения нормальных уравнений:

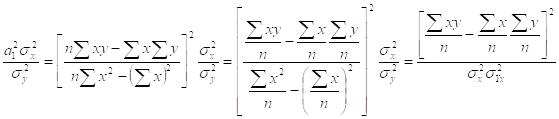
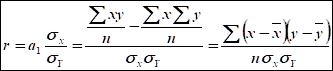
Коэфициент корреляции является частным случаем теоретического корреляционного соотношения , когда связь между СВ является линейной. В этом случае r является показателем тесноты связи.

- выборочный корреляционный момент

Выборочный коэфициент корреляции обладает свойствами:

1. r=0, если св Х и Y независимы

2. - Для любых св Х и Y

3. - Для случая линейной зависимости св Х и Y.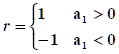

Коэфициент корреляции используется для оценки тесноты связи и в случае нелинейной зависимости между случайными величинами.

Если предварительный графический анализ поля корреляции указывает на какую либо тесноту связи, полезно вычислить коэфициент корреляции.

Если модуль коэфициента корреляции , то независимо от вида связи можно считать, что она достаточно тесна, чтобы исследоват ее форму.

< Предыдущая		Следующая >