54. Двумерное нормальное распределение
Его возникновение объясняется центральной предельной теоремой Ляпунова:

R – коэффициент корреляции. Х и У по отдельности распределены нормально (mx, sx) и (my, sy).
В частном случае независимых СВ Х и У r=0:
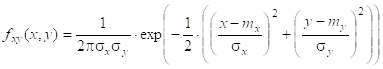
Исходные плотности одномерных нормальных распределений Х и У:
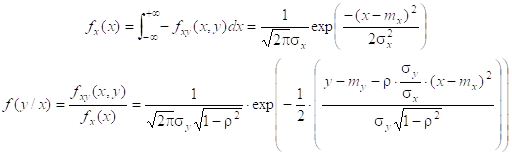
Условное распределение – нормальное с условиями:
![]() и
и ![]() .
.
Первое условие является уравнением функции регрессии.
![]() и
и ![]() .
.
Нормальная регрессия прямолинейна. Точность оценки у/х одинакова для всех х. В качестве меры тесноты связи используется коэффициент корреляции, а форму связи при этом характеризует коэффициент регрессии.
Z=fxy(x, y) – трехмерная поверхность, сечения которой плоскостями XZ и YZ представляют собой графики плотности одномерных распределений.
| < Предыдущая | Следующая > |
|---|