52. Определение эмпирического корреляционного соотношения
![]()
Y – измеряемое значение зависимой переменной
N – общее количество измерений
![]() - условное среднее (среднее значение зависимой переменной у в i-ом интервале св Х)
- условное среднее (среднее значение зависимой переменной у в i-ом интервале св Х)
K – общее количество интервалов
![]() - среднее всей совокупности измерений
- среднее всей совокупности измерений
В пределах каждого интервала, для всех тех значений Х, для которых есть экспериментальные результаты (значения Y), находим средние значения.
![]() Sy(x)2 – составляющая полной дисперсии, характеризует дисперсию результатов измерений относительно эмпирической линии регрессии, т. е. влияние прочих факторов на зависимую переменную Y.
Sy(x)2 – составляющая полной дисперсии, характеризует дисперсию результатов измерений относительно эмпирической линии регрессии, т. е. влияние прочих факторов на зависимую переменную Y.
Dy(x)2 – характеризует дисперсию эмпирической линии регрессии относительно среднего всей совокупности, т. е. влияние исследуемого фактора на зависимую переменную Y.
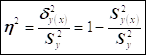 - Эмпирическое корреляционное соотношение
- Эмпирическое корреляционное соотношение
Из сравнения с формулой для теоретического корреляционного соотношения видно: при расчете Теоретического корреляционного соотношения Необходимо знать форму связи между переменными.
При вычислении эмпирического корреляционного соотношения никакие предположения о форме связи не используются, нужна только эмпирическая линия регрессии.
Свойства:
1. 0 £ ![]() £ 1
£ 1
2. если ![]() =1, все точки корреляционного поля лежат на линии регрессии – функциональная связь между Х и Y.
=1, все точки корреляционного поля лежат на линии регрессии – функциональная связь между Х и Y.
3. Если ![]() =0 (когда
=0 (когда ![]() ), отсутствует изменчивость условных средних
), отсутствует изменчивость условных средних ![]() , эмпирическая линия регрессии проходит параллельно оси абсцисс – свзи между Х и Y нет.
, эмпирическая линия регрессии проходит параллельно оси абсцисс – свзи между Х и Y нет.
Эмпирическое корреляционное соотношение ![]() завышает тесноту связи между переменными и случайными величинами, причем тем сильнее, чем меньше число измерений, поэтому
завышает тесноту связи между переменными и случайными величинами, причем тем сильнее, чем меньше число измерений, поэтому ![]() рекомендуется использовать для предварительной оценки тесноты связи, а для окончательной оценки – теоретическое корреляционное соотношение.
рекомендуется использовать для предварительной оценки тесноты связи, а для окончательной оценки – теоретическое корреляционное соотношение.
| < Предыдущая | Следующая > |
|---|