51. Измерение тесноты связи

Если бы величина Y полностью определялась аргументом Х, все точки лежали бы на линии регрессии. Чем сильнее влияние прочих факторов, тем дальше отстоят точки от линии регрессии. В случае в) связь между Х и Y является более тесной.

За основу показателя, характеризующего тесноту связи, берется общий показатель изменчивости дисперсии:

(*)

- дисперсия переменной Y относительно теоретической линии дисперсии, определяющей влияние прочих факторов на величину Y.

- условная дисперсия, характеризует дисперсию теоретической линии регрессии относительно условной генеральной средней my. Именно она определяет влияние данного фактора (Х) на величину Y и может быть использована для оценки тесноты связи между величинами Х и Y.

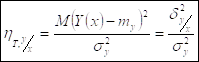- теоретическое корреляционное отношение.

Изменяется от 0 до 1, что легко доказать, поделив (*) на sу2:

1) Если =1, то

Влияние прочих факторов отсутствует. Все распределение будет сконцентрировано на линии регрессии. В этом случае между Х и Y существует простая функциональная зависимость.

2) Если =0, когда .

В этом случае линия регрессии Y по Х будет горизонтальной прямой, проходящей через центр распределения.

В случае, когда вид зависимости (форма связи) случайных величин Х и Y не установлен, часто бывает необходимо убедиться в наличии какой-либо связи вообще. Может оказаться, что связь несущественна и вычисление коэффициентов регрессии неоправданно.

Для объяснения такого вопроса вычисляется эмпирическое корреляционное отношение, определяемое на основе выборочных данных. При выводе формул для ЭКО пользуются эмпирической линией регрессии и оценкой дисперсии по выборке.

< Предыдущая		Следующая >