37. Проверка гипотезы о равенстве центров распределения математического ожидания 2-х нормальных генеральных совокупностей

Задача имеет большой практический интерес. Достаточно часто наблюдается такая ситуация, что средний результат в одной серии эксперимента отличается от среднего результата в другой серии эксперимента.

Возникает вопрос: можно ли объяснить отличительное расхождение случайными ошибками эксперимента и относительно малыми объёмами выборки или это отклонение вызвано какими-либо неизвестными, незамеченными закономерностями.

Имеется две случайных величин Х и Y с нормальным законом распределения.

Получим 2-е независимых выборки объёмом n1 и n2 из указанных генеральных совокупностей.

Необходимо проверить: Н0: М(X) = М(Y)

H1: |M(X) – M(Y)| > 0

Рассмотрим два случая:

1. – известны дисперсия генеральной совокупности ;

2. – дисперсия неизвестна .

1 - , M(X) и M(Y) - неизвестны, для их оценки мы используем средние выборочные

Относительно Известно, что они подчиняются нормальному закону распределения с параметрами:

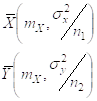
Рассмотрим случайную величину . В силу независимости выборок эта случайная величина подчиняется нормальному закону распределения.

Её дисперсия:

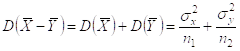
Если гипотез Н0 верна(справедлива), то тогда: .

Величина:

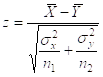с параметрами (0, 1)

Выбирая уровень значимости α или доверительную вероятность Р = 1- α можем записать:

; ;

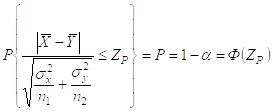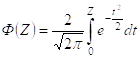Выбирая по величине интеграла вероятности значения ZP мы тем самым делим выборочных данных на область допустимых значений и критическую область.

Для области, где выполняется неравенство |Z| ≤ ZP – область допустимых значений(ОДЗ) Н0 – принимается.

А, если |Z| > ZP – критическая область(КО) Н0 – отвергается, Н1 – принимается.

Чем меньше α, тем меньше вероятность отклонить проверяемую гипотезе, если она верна. Но в этом случае увеличивается вероятность совершения ошибки II-го рода.

Чем меньше α, тем больше ОДЗ и тем больше вероятность принять проверяемую гипотезу, если она не верна, т. е. совершить ошибку II-го рода.

Методы проверки гипотез позволяют только отвергнуть проверяемую гипотезу, но они не могут доказать её справедливость.

< Предыдущая		Следующая >