38. 2 - Дисперсия неизвестна

Есть 2-е случайных величины X и Y, .

mx и my неизвестны берутся независимые выборки (n1;n2) и рассматривается гипотеза: Н0: M(X) = M(Y)

H1: |M(X) – M(Y)| > 0.

Для оценки математического ожидания M(X) и M(Y) используем среднее выборочное . Для оценки дисперсий используем:

- несмещённые, состоятельные оценки дисперсии.

Поскольку генеральные совокупности X и Y имеют одинаковые дисперсии, то для оценки дисперсии Целесообразно использовать результаты обеих выборок.

Наиболее целесообразной оценкой дисперсии является средняя взвешенная этих двух оценок.

Если гипотеза Н0 справедлива, то тогда случайная величина Подчиняется нормальному закону распределения с и с дисперсией

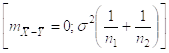
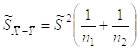
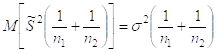
Если построить случайную величину:

, то она будет подчиняться нормальному закону с параметрами (0; 1).

Т. к. неизвестна, то такая величина подчиняется t-распределению Стьюдента(со степенями свободы n1 + n2 – 2).

Для α(Р = 1– α) подсчитывается критическое значение

Если вычисленные значения , то гипотеза Н0 отвергается и наоборот:

Н0 принимается.

< Предыдущая		Следующая >