34. Построение доверительного интервала для математического ожидания

Случайная величина Х распределённая с параметрами (m, σ2).

Математическое ожидание неизвестно и требуется построить для него доверительный интервал.

1. Известно σ2.

2. Неизвестно σ2.

1. σ2 известно.

Проводится выборка из генеральной совокупности и в качестве несмещённой, состоятельной и эффективной оценки математического ожидания выбирается . Оно тоже подчиняется нормальному закону с параметрами:

, где: n – объём выборки.

Нормированная величина:

Подчиняется нормальному закону распределения с параметрами (0; 1), тогда вероятность:

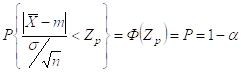
Вероятность задаётся уровнем α, величина Р – доверительная вероятность. По таблице находим величину Zp.

При известном Zp получим:

Интервал для математического ожидания (m*; m*) получим:

– Доверительный интервал для математического ожидания с уровнем значимости α.

2. σ2 неизвестно.

Точно так же проводится выборка объёмом n, формируется случайная величина t

Случайная величина t имеет распределение Стьюдента.

Зная объём выборки n, задаваясь уровнем значимости α или задаваясь доверительной вероятностью р=1-α.

По распределению Стьюдента находим tn, p – максимальное отклонение m и .

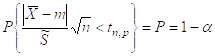
Где: Р – доверительная вероятность.

Отсюда легко строится доверительный интервал.

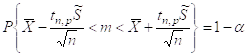
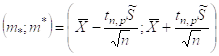
Несмотря на кажущиеся совпадения двух формул они существенно отличаются друг от друга.

Во втором случае величина доверительного интервала зависит не только от доверительной вероятности, но и от объёма выборки.

Это различие наиболее существенно проявляется при малых выборках.

< Предыдущая		Следующая >