33. Когда случайная величина Х с параметрами (m, σ2) – неизвестны

Для оценки дисперсии генеральной совокупности используется величина:

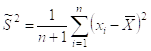
Случайная величина Имеет распределение χ2 с к = n – 1 степенями свободы.

Уменьшение степени свободы использована для получения среднего выборочного.

Доверительный интервал.

Рассмотренные ранее оценки получили название точечных оценок. На практике широко используются интервальные оценки, для получения которых используется метод доверительных интервалов.

В методе доверительных интервалов указывает не одно(точечное) значение интересующего нас параметра, а целый интервал. Он строится на основе неравенства Чебышева:

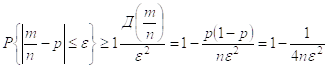
Задаётся некоторое число 0 < α < 1 близкое к нулю, которое называется Уровень значимости.

Параметр ε находится из неравенства:

, тогда:

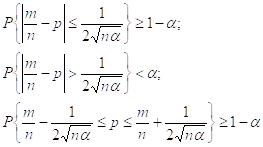
Интервал называется Доверительным интервалом с уровнем значимости α.

Доверяясь расчёту мы утверждаем, что неизвестная вероятность принадлежит указанному интервалу, а вероятность возможной ошибки имеющей место тогда, когда этот интервал не накрывает истинное значение α не превосходит уровня значимости α.

N = 1000, m/n = 0,6

При α = 0,1 (0,550; 0,650)

При α = 0,01 (0,442; 0,758)

Истинное значение вероятности Р мы незнаем, но можем утверждать, что первый интервал накрывает это значение с вероятностью не менее чем 0,9 , а второй – 0,99.

Пример. Имеется некоторое предположение, гипотеза, о том, что неизвестная вероятность Р равна заданному число Р0:

Н0: р = р0; (Р0 = 0,5).

Эту гипотезу можно принять, а можно и отклонить посчитав её противоречащей известным статистическим данным.

Для принятия решения(проверки гипотезы) мы проделаем следующую процедуру:

Если Р0Î(Р*, Р*) с α, то гипотезу принимаем(возможно здесь и ошибка, мы можем принять ложную гипотезу – такая ошибка первого рода).

Если Р0Ï (Р*, Р*) с α, то гипотеза отвергается(здесь тоже можем совершить ошибку отклонить верную гипотезу – такая ошибка второго рода, вероятность такой ошибки заранее задаётся нами при построении доверительного интервала).

При наших предположениях, когда уровень значимости равен 0,1 в общем мы имеем Р0Ï (0,550; 0,650). Эта гипотеза отвергается, при этом мы ошибаемся не более чем в 1 случае из 10.

< Предыдущая		Следующая >