32. Распределение дисперсии в выборках нормальной совокупности. Распределение χ2 Пирсона
Выборочная дисперсия так же является случайной величиной меняющейся от выборки к выборки.
1) М(Х) – известно;
2) М(Х) – не известно.
1) Имеется случайная величина Х, которая подчиняется нормальному закону с параметрами (m, σ2),
Где: хi(i = 1, 2, …, n) – независимые наблюдения над случайной величиной.
Для дисперсии мы выбираем вот такую оценку:
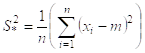 - несмещённая, состоятельная и эффективная оценка дисперсию генеральной совокупности.
- несмещённая, состоятельная и эффективная оценка дисперсию генеральной совокупности.
![]()
Величина Ui является случайной величиной с параметрами (0;1).

Случайная величина представляющая собой сумму квадратов n независимых случайных величин, каждая из которых подчиняется нормальному закону распределения с параметрами (0;1) и независимых случайных величин с распределением χ2 с к = n – степенями свободы.
Сама функция плотности вероятности f(χ2) имеет вид:
![]()
Эта функция зависит только от объёма выборки и не зависит ни от математического ожидания, ни от дисперсии, ни от х.
Имеются таблицы распределения χ2 позволяющие вычислить вероятность события![]()
![]() ,
,
Где: к – число степеней свободы;
α – доверительная вероятность, которая задаётся самим исследователем.
2) Математическое ожидание неизвестно.
| < Предыдущая | Следующая > |
|---|