10. Предельные теоремы в схеме Бернулли
1. Предельная теорема Пуассона. При р»0, n-велико, np= l £ 10.
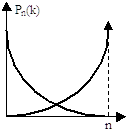
![]()
Формула дает распределение Пуасона, описывает редкие события.
2. Предельная теорема Муавра-Лапласа.
0 £ p £ 1, n –велико, np>10
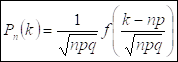
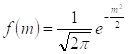 - стандартное нормальное распределение
- стандартное нормальное распределение
3. Предельная интегральная теорема Муавра-Лапласа.
В условиях предыдущей теоремы вероятность того, что событие А в серии из n испытаний наступит не менее k1 раз и не более k2 раз:
![]()
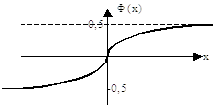
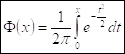 - функция Лапласа
- функция Лапласа
![]()
Следствие:
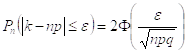
![]()
![]()
Пример. ОТК проверяет на стандартность 1000 деталей. Выбранная деталь с вероятностью р=0,975 является стандартной.
1) Найти наивероятнейшее число стандартных деталей:
K0=np=975
2) Найти вероятность того, что число стандартных деталей среди проверенных отличается от k0 не более чем на 10.
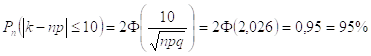
3) С вероятностью 0,95 найти максимальное отклонение числа стандартных деталей среди проверенных.
![]()
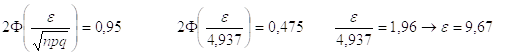
4) Найти число проверяемых деталей n, среди которых с вероятностью 0,9999 стандартные детали составят не менее 95%.
0,95n £ k £ n
P(0,95n £ k £ n)=0.9999 = Ф(х2)- Ф(х1) = 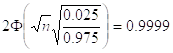
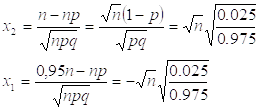
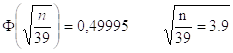 n=3.92*39=594
n=3.92*39=594
При р=0,9999 n=594
При р=0,999 n=428
При р=0,99 n=260
| < Предыдущая | Следующая > |
|---|