09. Схема последовательных испытаний Бернулли

Проводится серия из n испытаний, в каждом из которых с вероятностью р может произойти событие А, с вероятностью q=1-р событие .

Вероятность наступления события А не зависит от числа испытаний n и результатов других испытаний.

Такая схема испытаний с двумя исходами (событие А наступило либо не наступило) называется Схемой последовательных испытаний Бернулли.

Пусть при n испытаниях событие А наступило k раз, (n-k) раз событие .

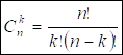- число различных комбинаций события А

Вероятность каждой отдельной комбинации:

Вероятность того, что в серии из n испытаний событие А, вероятность которого равна р, появится k раз:

- условие нормировки.

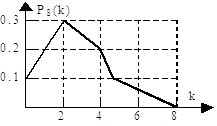Пример. Вероятность изготовления нестандартной детали равна р=0,25, q=0.75. Построить многоугольник распределения вероятностей числа нестандартных деталей среди 8 изготовленных.

N=8 p=0.25 q=0.75

Если K0 – наивероятнейшее число, то оно находится в пределах:

Np-q £ k0 £ np+q

Если число (np+q) нецелое, то k0 – единственное

Если число (np+q) целое, то существует 2 числа k0.

< Предыдущая		Следующая >