06.1. Метод Квайна;— Мак-Класки нахождения сокращённой ДНФ двоичной функции

Пусть Функция F задана в виде СДНФ. Метод, предложенный Квайком в 1952 г. заключается в следующем:

1) применим к Элементарным конъюнкциям СДНФ операцию «неполного склеивания»: , до тех пор, пока в результате применения этой операции не перестанут появляться новые конъюнкции;

2) в полученной ДНФ выполняем операции поглощения: , пока это возможно.

Теорема 6.1. В результате выполнения пунктов 1, 2 получается сокращённая ДНФ функции F.

Доказательство. Сначала заметим, что из всякой Импликанты функции F можно с помощью «операции расклеивания» получить дизъюнкцию импликант длины N. Поскольку все импликанты длины n входят в СДНФ, то в результате применения операции неполного склеивания в СДНФ на первом этапе (пункт 1) метода будут получены все, в том числе и простые, импликанты функции F.

После применения второго этапа (пункт 2), очевидно, в ДНФ останутся только простые импликанты, т. е. полученная в результате ДНФ будет сокращенной. Теорема доказана.

Мак-Класки в 1956 г. предложил удобную интерпретацию этого метода. Прежде всего заметим, что склеиваться могут только конъюнкции одинакового ранга, отличающиеся по одной переменной. Будем записывать конъюнкции в виде вектора (). Индексом конъюнкции назовём .

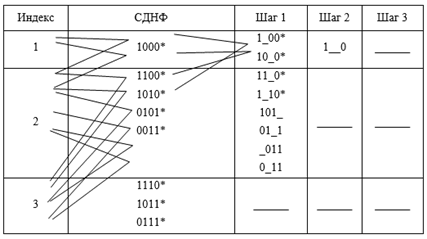
Учитывая это замечание, разобьём все импликанты в СДНФ на группы в соответствии со значениями их индексов. Сам метод при этом заключается в заполнении таблицы специального вида (табл.6.1).

Таблица 6.1

Пример 6.2. Пусть F — функция, геометрическое представление которой дано на рис.5.1. Её СДНФ имеет вид:

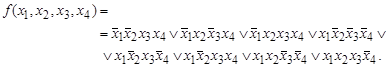
Применяя операцию неполного склеивания к импликантам длины N (СДНФ) производим заполнение колонки табл.6.1. При этом в СДНФ звёздочкой отмечаются использованные импликанты (они будут поглощаться на втором этапе). Затем операция склеивания применяется к конъюнкциям ранга (N – 1) и т. д. Как только заполнение таблицы прекратилось, выбираются все не отмеченные звёздочкой импликанты и из них составляется сокращённая ДНФ. Для рассмотренного примера сокращённой ДНФ будет:

< Предыдущая		Следующая >