05.2. Геометрическая интерпретация минимизации ДНФ
Зададим двоичную функцию на N-мерном двоичном кубе. Как было отмечено ранее, при таком задании элементарным конъюнкциям ранга K соответствуют такие множества вершин, графы связности которых имеют вид (K – N)-мерных кубов. Поскольку дизъюнкции элементарных конъюнкций соответствует объединение множеств вершин таких подкубов, то каждой ДНФ функции F соответствует некоторое покрытие множества MF единичных вершин функции F (области истинности) подмножествами, имеющими в качестве графов связности подкубы. Простым импликантам функции F будут соответствовать подкубы максимальных размерностей, покрывающие вершины из MF.
Соответственно, Первая задача (1-й этап) решается перечислением всех максимальных подкубов, содержащихся в графе связности множества MF. Вторая задача (2-й этап) заключается в нахождении минимальных (по числу подкубов) покрытий множества MF максимальными подкубами.
Рассмотрим пример. Пусть двоичная функция F (X1, X2, X3, X4) имеет геометрическое задание, изображённое на рис.5.1.
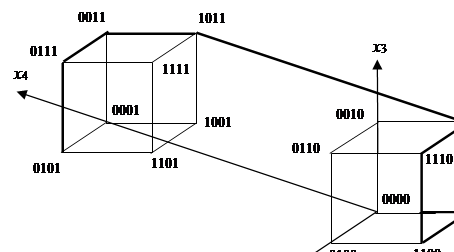
Рис.5.1
Граф связности такой функции имеет вид рис.5.2.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис.5.2
Выпишем сокращённую ДНФ, записывая простые импликанты в том же порядке, в каком они изображены в графе связности:
Легко видеть, что тупиковыми будут две ДНФ:
Соответствующие покрытиям (рис.5.3).

Рис.5.3
Минимальной будет только вторая тупиковая ДНФ.
| < Предыдущая | Следующая > |
|---|