03.3. Критерий полноты системы булевых функций

Теорема 3.27. Система булевых функций полна тогда и только тогда, когда она содержит хотя бы по одной функции каждого из следующих классов:

, , , ,

(без доказательства).

Пример 3.28. Пусть функция задана табл.3.3.

Таблица 3.3

0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

Показать, что — шефферова функция, т. е.  — полная система, т. е. . Выразить и формулами над К.

Решение:

,

Но не

.

Чтобы выяснить вопрос о принадлежности классу , представим многочленом Жегалкина:

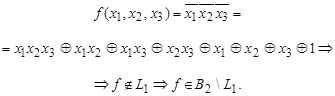
Итак, все условия теоремы 3.27 выполнены. Следовательно  — полная система, т. е.  — шефферова функция.

Теперь решим вторую часть примера. Так как , то очевидно , .

< Предыдущая		Следующая >