03.2. Замкнутые классы булевых функций

Определение 3.15. Класс булевых функций называется замкнутым, если он совпадает со своим замыканием, т. е. .

Замечание 3.16. Полное описание всех замкнутых классов было дано американским математиком Э. Постом. В частности, он доказал, что множество всех замкнутых классов булевых функций счетно и в каждом замкнутом классе можно выделить конечную подсистему , порождающую , т. е. имеющую своим замыканием класс , т. е. .

Определение 3.17. Булева функция называется функцией, Сохраняющей константу 0, если .

Класс всех булевых функцией, сохраняющих константу 0, обозначим .

Определение 3.18. Булева функция называется функцией, Сохраняющей константу 1, если .

Класс всех булевых функцией, сохраняющих константу 1, обозначим .

Определение 3.19. Булева функция называется Линейной, если , такие, что

.

Класс всех булевых линейных функций обозначим через .

Определение 3.20. Булева функция называется Аффинной функцией, если , такие, что .

Обозначим через класс всех булевых аффинных функций.

Определение 3.21. Булева функция называется Самодвойственной функцией, если

. (3.1)

Класс всех булевых самодвойственных функций обозначим через S.

Далее определим понятие Монотонной функции. Для этого нам необходимы некоторые дополнительные сведения. Изложим их. На множестве введем отношение , положив для наборов и :

,

Где отношение на понимается как неравенство на множестве чисел {0, 1}.

Несложно доказать, то отношение рефлексивно, транзитивно и антисимметрично, т. е. является отношением частичного порядка.

Определение 3.22. Булева функция называется Монотонно возрастающей или Монотонной, если для любых наборов выполняется условие: .

Замечание 3.23. Нульместные функции 0 и 1 также естественно считать монотонными.

Класс всех булевых монотонных функций обозначим через М.

Утверждение 3.24. Классы булевых функций и являются замкнутыми классами булевых функций.

Для доказательства данного утверждения нам необходимо определить понятие ранга формулы над классом .

Определение 3.25. Число всех символов функций из , встречающихся в формуле над , называется рангом формулы и обозначается через .

Замечание 3.26. Понятие ранга формулы над классом не следует путать с понятием ранга элементарной конъюнкции из определения 2.1.

Доказательство утверждения 3.24. Замкнутость перечисленных в утверждении 3.24 шести классов функций доказывается по одной и той же схеме. Проделаем это для какого-нибудь одного класса, например S.

Согласно определениям замыкания (определение 3.1) и замкнутого класса (определение 3.15) нам необходимо доказать, что любая функция, представимая формулой над S, принадлежит S. Докажем это индукцией по рангу формулы А, представляющей функцию .

Если , то , и утверждение очевидно, так как .

Пусть утверждение верно для всех , таких что , где .

Докажем, что утверждение верно и при . Если , то А имеет вид: , где и  — формулы меньших рангов, чем , т. е. . По предположению индукции формулы представляют булевы функции . Тогда для любых имеем:

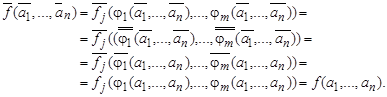
Следовательно, удовлетворяет условию (3.1), т. е

< Предыдущая		Следующая >