10. Понятие о теории моделей

Теория моделей возникла на стыке между алгеброй и математической логикой. Она занимается в основном изучением таких свойств классов алгебраических систем, которые могут быть записаны формулами какого-либо логического исчисления (чаще всего, исчисления предикатов). При этом сами алгебраические системы изучаемого класса становятся интерпретациями или моделями соответствующего исчисления. Из анализа связей между формальным языком (формальными выводами, доказательствами и т. п.) и его интерпретациями черпает теория моделей и главные средства исследований. В самостоятельную область математики теория моделей выделилась в 50-е годы XX века благодаря работам Мальцева, Тарского, Геделя, Левенгейма, Скулема, Биркгофа и др.

К настоящему моменту теория моделей является достаточно развитой областью математики со своей проблематикой и собственными методами исследований. Многие из разработанных в ней методов успешно используются в других областях математики.

С некоторыми такими методами мы познакомимся в данной лекции.

Предварительно сделаем одно замечание о предикате равенства и дадим несколько определений. Пусть К — некоторый класс алгебраических систем сигнатуры σ. Тогда можно построить язык логического исчисления в сигнатуре σ и записать свойства систем из класса К формулами полученного исчисления. Однако формализация свойств систем зачастую существенно облегчается, если в сигнатуру исчисления ввести еще двухместный предикат равенства « = ». Полученную сигнатуру будем обозначать в виде σ^. Сразу отметим, что, введя предикат равенства, мы должны пополнить и систему аксиом исчисления, введя в нее аксиомы, характеризующие предикат равенства. В качестве таких аксиом выбираются формулы:

"X(X = X),

"X1, X2 (X1 = X2 ® X2 = X1),

"X1, X2, X3 (X1 = X2 & X2 = X3 ® X1 = X3),

Характеризующие отношение равенства как отношение эквивалентности, а также все формулы вида

"X1, …, XK, Y1, …, YK (X1 = Y1 & … & XK =

= YK ® H(X1, …, XK) = H(Y1, …, YK));

"X1, …, XN, Y1 ,…, YN (X1 = Y1 & … & XN = = YN ® (P(X1, …, XN) = P(Y1, …, YN))),

Где H — функциональный, а Р — предикативный символы из σ. Последние формулы характеризуют согласованность отношения равенства со всеми предикатами и операциями из σ. Ниже мы будем рассматривать лишь исчисления с равенством и аксиомы равенства будут автоматически включаться в соответствующие системы аксиом.

Определение 10.1. Пусть K — класс алгебраических систем сигнатуры σ. Множество замкнутых формул исчисления предикатов сигнатуры σ^, истинных во всех системах из K, называется элементарной теорией класса K и обозначается th(K) или th(А), если K состоит из одной алгебраической системы А.

Например, можно говорить об элементарной теории арифметики натуральных чисел, об элементарной теории групп, об элементарной теории конечных полей и т. д. Заметим, что слово «элементарная» в термине «элементарная теория» объясняется тем, что любая формула исчисления предикатов выражает свойства систем через указание связей между их элементами, поскольку кванторы навешиваются лишь на предметные переменные.

Задача описания элементарной теории th(K) для разных классов K является важнейшей задачей теории моделей. В частности, теория th(K) является разрешимой, если существует алгоритм, позволяющий для любой формулы исчисления в сигнатуре σ^ выяснить, содержится она в th(K) или нет. В противном случае элементарная теория называется неразрешимой. В решении вопросов о разрешимости или неразрешимости элементарных теорий теория моделей смыкается с теорией алгоритмов, которая будет изучаться в последующих лекциях.

Определение 10.2. Пусть F — произвольное множество формул исчисления предикатов сигнатуры σ^. Алгебраическая система А сигнатуры σ, на которой истинны все формулы из F, называется моделью для F, что записывается в виде

А╞═ F.

Вопросы, связанные с построением и исследованием моделей для заданных систем формул, также занимают важное место в теории моделей. В частности, алгебраические системы сигнатуры σ называют элементарно эквивалентными, если в них истинны одни и те же формулы исчисления предикатов сигнатуры σ^. Очевидно, что из изоморфизма систем следует их элементарная эквивалентность. Обратное же не всегда верно.

В связи с этим укажем на одну из долго стоящих и широко известных проблем А. Тарского (проблему о полноте для элементарной теории свободных групп): будут ли элементарно эквивалентными свободные группы рангов M и N при M > N > 1.

Определение 10.3. Класс К алгебраических систем сигнатуры σ называется аксиоматизируемым (конечно аксиоматизируемым), если существует такое множество (конечное множество) формул F исчисления предикатов сигнатуры σ^, что А Î К Û А╞═ F. При этом множество F называется системой аксиом класса К.

Очевидно, что наличие хорошей системы аксиом, описывающих класс алгебраических систем, играет немаловажную роль для изучения этого класса. В связи с этим в теории моделей вопросу аксиоматизируемости уделяется серьезное внимание. Приведем несколько примеров аксиоматизируемых классов.

1. Класс всех групп в сигнатуре σ = <·, 1> конечно аксиоматизируем. Системой аксиом может служить множество формул AGr:

1) "X1, X2, X3 ((X1 · X2) · X3 = X1 · (X2 · X3)),

2) "X1 (X1 · 1 = X1),

3) "X1 $X2 (X1 · X2 = 1).

Добавление к ним формулы

4) "X1, X2 (X1 · X2 = X2 · X1)

Приводит к аксиоматике класса всех абелевых групп.

2. Класс всех полей в сигнатуре σ = <+, ·, 0, 1> конечно аксиоматизируем. Его система аксиом AF может быть получена добавлением к аксиомам абелевых групп в сигнатуре <+, 0>, выписанных в примере 1, формул 1, 2, 4, характеризующих коммутативные полугруппы с единицей, и формулы

"X1 (X1 ¹ 0 ® $X2(X1 · X2 = 1)).

Добавив к системе аксиом AF еще аксиому

,

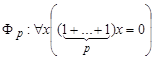(Р — простое число), мы выделим из всех полей класс полей характеристики Р.

Класс полей характеристики 0 задается системой аксиом, полученных добавлением к системе АF отрицаний аксиом ФP по всем простым числам Р. Эта система аксиом бесконечна. Можно доказать, что класс полей характеристики 0 не является конечно аксиоматизируемым.

3. Арифметику натуральных чисел можно рассматривать как алгебру сигнатуры σA = {+, ·, `, 1}, где «`» есть символ унарной операции. Объединяя систему аксиом Пеано с требованием к операциям сложения и умножения по Грассману, получим следующую систему аксиом — формул:

"X1(X1` = 1),

"X1, X2 (X1 = X2 ® X1` = X2`),

"X1, X2 (X1` = X2` ® X1 = X2),

"X1 (X1 + 1 = X`),

"X1, X2 (X1 + X2`) = (X1 + X2)`,

"X1(X1 · 1 = X1),

"X1, X2 (X1 · X2` = X1 · X2 + X1),

A(1) &"X1(A(X1) ® A(X1`)) ® "YA(Y),

Где А — произвольная формула сигнатуры σA.

Пусть K — произвольный аксиоматизируемый класс алгебраических систем сигнатуры σ, и А — его система аксиом. Тогда, добавив к аксиомам исчисления предикатов аксиомы равенства и все аксиомы из А, мы построим новое логическое исчисление αК. В нем, как и в изученном нами исчислении предикатов α, можно определить понятия формулы, выводимой из заданной системы формул, доказуемой формулы и т. д.

Алгебраические системы класса К будут являться такими интерпретациями исчисления αК, в которых истинны все формулы из А, т. е. будут моделями множества А. Для исчисления αК, как и для исчисления α, доказывается следующая теорема о полноте. Если Ф — замкнутая формула исчисления αК, то

Ф Î th(K) Û	├─ Ф.
	αК

Эту теорему, с одной с стороны, можно использовать для проверки истинности формулы Ф на системах класса K, а с другой стороны, из нее следует ряд общих методов получения утверждений об алгебраических системах. Один из этих методов, называемый методом компактности, основан на локальной теореме Мальцева для любого исчисления αК, называемой также теоремой компактности.

Множество формул исчисления αК выполнимо тогда и только тогда, когда выполнимо любое его конечное подмножество.

Первые примеры по применению этой теоремы были указаны в теории групп самим Мальцевым. Ниже мы приводим один его результат.

Пусть G — группа и G2 < G1 < G. Охарактеризуем сначала формулами утверждения:

1. GI < G – GI — подгруппа группы G.

2. G2 < G1.

3. G2  G1 – G2 — нормальный делитель группы G1.

4.  — факторгруппа.

С этой целью введем на G два одноместных предиката R1 и R2, положив:

RI(X) = И Û X Î GI, I = 1, 2.

Тогда утверждения 1 – 3 запишутся формулами:

"X1, X2, X3(RI(X1)RI(X2)(X2X3 = 1) ® RI(X1X3)),

"X(R2(X) ® R1(X)),

"X1, X2, X3(R1(X1)R2(X2)(X1 X3 = 1) ® R2(X3X2X1)).

На элементы фактор-группы можно смотреть как на элементы группы G1, определив иначе предикат равенства E(X, Y) элементов X, Y из G1 (как принадлежность их к одному смежному классу по G2):

E(X1, X2) Û $X3(R2(X3)(X3X2 = X1)).

И несколько иначе, чем в G1 определим операцию «°» умножения элементов из G1

X1 ° X2 = X3 Û $X4 (R2(X4)(X1X2 = X3X4)).

Легко видеть, что операция «°» определена корректно, и если какое-либо групповое свойство Р группы G1 выражено формулой В в сигнатуре σ = {R1, R2, =, ·, 1}, то, заменив в В предикат «=» на Е и операцию · на °, мы получим формулу Р*, выражающую групповое свойство факторгруппы (т. е. если Р истинна на G1, то Р* истинна на ).

Пусть теперь Р = [P1, …, PK] — набор свойств группы G, записываемых конечными системами замкнутых формул и сохраняющихся при переходе к подгруппам.

Пусть группа G имеет тип Р, т. е. в ней существует нормальный ряд

(10.1)

Такой, что обладает свойством PI, I = 1, …, K.

Как и выше, введем на группе G одноместные предикаты R1, R2, …, RK, характеризующие подгруппы G1, G2, …, GK и образуем множество формул АG в сигнатуре σ1, состоящей из предикатов R1, R2, …, RK, «=», бинарной операции · и нуль-арных операций, отвечающих всем элементам группы G, т. е. всех констант из группы G, включив в него:

1) систему аксиом АGr;

2) формулы " X1, X2 (X1 = X2 ® RI(X1) = RI(X2));

3) формулы, характеризующие утверждения , I = = 0, …, K – 1;

4) формулу "X (RK(X) ® X = 1), утверждающую, что GK = 1;

5) формулы для записи того факта, что фактор-группа обладает свойством РI.

Введем еще для группы G систему формул D(G), называемую диаграммой группы G. Для любых элементов GI, GJ, GR ΠG D(G) содержит формулу GIGJ = GR, если она истинна в G, и формулу GIGJ ¹ GR — в противном случае. Объединение систем АG и D(G) обозначим через KG.

Очевидно, что G имеет тип Р тогда и только тогда, когда множество формул KG выполнимо, т. е. имеет модель.

Теорема 10.4. Если каждая конечно порожденная подгруппа H < G имеет тип Р, то и G имеет тип Р.

Доказательство. Согласно локальной теореме Мальцева для выполнимости множества формул KG достаточно доказать выполнимость любого его конечного подмножества. При этом из конечных систем достаточно рассматривать лишь подсистемы, содержащие АG.

Итак, пусть D` — конечная подсистема из D(G), G` — множество элементов из G, участвующих в соотношениях из D`, и Н — подгруппа в G, порожденная множеством G`. Так как Н — подгруппа типа Р, то множество формул АG U D(H), а потому и АG È D1’ выполнимо, и теорема доказана.

Примеры.

1. Возьмем в качестве свойства PI формулу "X, Y (Xy = Yx). Тогда группы типа Р — это в точности разрешимые группы ступени разрешимости N < K и потому получается теорема.

Теорема. Если каждая конечно порожденная подгруппа группы G разрешима ступени N < K, то и G — разрешимая группа ступени N < K.

2. Возьмем в качестве Р1 свойство: группа содержит не более N элементов, а в качестве Р2 — любую формулу, выводимую из АGr. Тогда получится теорема.

Теорема. Если каждая конечно порожденная подгруппа группы G содержит нормальный делитель индекса K £ N, то G также содержит нормальный делитель индекса K £ N.

Таким образом, выбирая различные свойства PI, мы будем получать различные утверждения о группах на основании свойств только конечно порожденных подгрупп.

Проиллюстрируем на примере еще один метод теории моделей для получения утверждений об алгебраических системах, называемый методом переноса.

Теорема 10.5. Если В — замкнутая формула в сигнатуре теории полей и В истинна на всех полях характеристики 0, то существует такое простое число Р0, что В истинна на любом поле характеристики P > Р0.

Доказательство. Действительно, если В истинна на всех полях характеристики 0, то В выводима из множества формул АF È {: Р = 2, 3, 5, …}. Однако в выводе формулы В используется лишь конечное множество аксиом вида :

, .

Тогда В выводима из систем аксиом АF È T, и потому истинна на всех полях, кроме полей характеристики , и, в частности, всех полях характеристики P > Р0.

Выбирая в качестве В различные формулы, мы будем получать различные конкретные утверждения. В частности, можем получить следующий интересный факт. Если система алгебраических уравнений

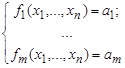(10.2)

Над кольцом Z не имеет решений в любом расширении поля рациональных чисел, то существует такое простое число Р0, что при каждом простом P > Р0 система уравнений, полученная заменой в (10.2) всех коэффициентов их вычетами по модулю Р не имеет решений в любом поле характеристики Р.

< Предыдущая		Следующая >