64. Матрица линейного оператора

Пусть задан линейный оператор , переводящий x Î L1 в y Î L2: .

Выберем в L1 базис e1 e2 … en и в L2 базис g1 g2 … gm

.

Т. е. для задания оператора достаточно задать только образы базисных векторов, т. е. Е1, Е2, …, Еn.

Положим, что эти образы есть

Составим матрицу:

Тогда из вышесказанного следует:

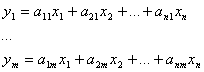
Или Y = A X

Матрица А, транспонированная АT называется матрицей линейного оператора, k-й столбец этой матрицы составлен из координат вектора Еk в базисе g1 g2 … gm.

Оказывается, что некоторые характеристики этой матрицы не зависят от базисов и характеризуют внутренние свойства оператора. Так, запишем без доказательства, что ранг матрицы линейного оператора равен размерности пространства образов. Будем называть этот ранг – рангом линейного оператора. Если этот ранг совпадает с размерностью пространства L, или размерность пространства образов совпадает с размерностью пространства прообразов, то оператор назовем невырожденным.

Если множество образов и множество прообразов принадлежат одному и тому же пространству, то будем говорить о преобразовании пространства само в себя а оператор этого преобразования будем называть оператором линейного преобразования или линейный оператор. В дальнейшем мы будем рассматривать линейные операторы и употреблять термин операторы.

< Предыдущая		Следующая >