61. Ортогональные матрицы и их свойства
Рассмотрим теперь, какими свойствами обладает матрица перехода от одного ортонормированного базиса к другому в евклидовом пространстве. Вспомним перехода от одного базиса к другому: если ![]() , то
, то ![]() . Матрицу АТ мы называли матрицей перехода от одного базиса к другому. Столбцы этой матрицы представляют собой координаты векторов
. Матрицу АТ мы называли матрицей перехода от одного базиса к другому. Столбцы этой матрицы представляют собой координаты векторов ![]() в базисе
в базисе ![]() .
.
Введем сначала определение: матрица Т с вещественными коэффициентами называется ортогональной, если Т’ = T-1 – транспонированная матрица равна обратной. Т. е. Т Т’ = T’ T = E. Отсюда следует det (T T’) = det T × det T’ = det E = 1 или det T = ±1.
Обратная матрица T-1 также ортогональна:
![]() , или
, или ![]() .
.
Запишем еще свойства ортогональной матрицы, вытекающие из того, что
![]() , или:
, или:
![]()
Или: 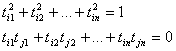 сумма квадратов элементов какой – либо строки (или столбца) равна 1, а сумма произведений соответствующих элементов разных строк (столбцов) равна 0.
сумма квадратов элементов какой – либо строки (или столбца) равна 1, а сумма произведений соответствующих элементов разных строк (столбцов) равна 0.
Предположим, имеем два ортонормированных базиса в евклидовом пространстве: ![]() и
и ![]() . Если
. Если ![]() , то координаты некоторого вектора Х в старом базисе х и новом х’ связаны соотношением:
, то координаты некоторого вектора Х в старом базисе х и новом х’ связаны соотношением: ![]() , где АT – матрица перехода.
, где АT – матрица перехода.
Теорема: матрица перехода от одного ортонормированного базиса к другому является ортогональной.
Доказательство: положим имеем два вектора
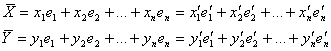
Запишем матрицы – столбцы координат этих векторов:

Скалярное произведение этих двух векторов:
![]() , или, в матричной записи:
, или, в матричной записи:
![]() (*)
(*)
Если матрица перехода от одного базиса ![]() к другому
к другому ![]() есть S, то:
есть S, то:
X = S X1 ; Y = S Y1
Подставим в (*):
![]()
Отсюда ST×S = E или ST = S-1. Т. е. матрица S – ортогональная.
К примеру, матрица, осуществляющая поворот осей координат в одной из предыдущих лекций – это матрица перехода от одного ортонормированного базиса к другому. Она является ортогональной.
![]()
![]()
detT = 1, T-1 = T` = ![]()
| < Предыдущая | Следующая > |
|---|