60. Ортонормированный базис конечномерного. Евклидового пространства

В линейном пространстве, как мы установили в предыдущих лекциях, существует базис – любые n линейно независимых векторов. Все базисы были одинаковы. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортонормированными базисами. Введем определение ортонормированного базиса: будем говорить, что k элементов E1, e2, … en n – мерного евклидового пространства Е образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т. е. если

Существует теорема: во всяком n – мерном евклидовом пространстве E существует ортонормированный базис.

Доказательство: согласно определению размерности в пространстве E найдется n линейно независимых векторов f1, f2, …, fn. Докажем, что можно построить n элементов E1, e2, … en, линейно выражающихся через f1, f2, …, fn и образующих ортонормированный базис.

Определим вектор E1 Как нормированный вектор f1, E1*=F1:

Построим вектор E2 так, чтобы он был ортогонален вектору E1:

Умножим скалярно на E1:

Вектор E3 определим следующим образом:

Коэффициенты b1 и b2 найдем из условия ортогональности вектора е3 к вектору е1 и вектору е2:

Отсюда: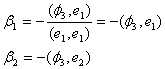

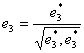, где

Продолжая этот процесс n раз, получим для вектора en:

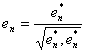, где или

Т. о. мы доказали теорему, что во всяком пространстве Е существует ортонормированный базис. В процессе доказательства мы построили этот базис. Процесс построения называется ортогонализация или процесс ортогонализации.

В ортонормированном базисе скалярное произведение векторов равно сумме произведений координат этих векторов – этим свойством мы уже пользовались в векторной алгебре:

(x, y) = x1y1 + x2y2 +… + xnyn

Действительно:

< Предыдущая		Следующая >