59. Норма вектора. Нормированное пространство

Определим длину или норму вектора, которую обозначим

,

Здесь учтена аксиома 40 и берется арифметическое значение корня. Из определения нормы вытекает:

1) |x| > 0 при x ¹ 0 и |x| = 0 только, если x = 0.

2) |l x| = |l| |x|

Вектор X, длина которого равна единице, называется нормированным. Очевидно, всякий ненулевой вектор можно пронормировать, умножив его на число . Полученный вектор будет нормированным.

Определим угол между векторами. Углом между векторами назовем угол, косинус которого определяется из соотношения

В силу неравенства Коши – Буняковского |cos j| £ 1, что корректно.

Договоримся считать два вектора евклидового пространства х и у ортогональными, если их скалярное произведение равно нулю. Отсюда следует, что в евклидовом пространстве справедлива теорема Пифагора:

|| x + y ||2 = (x + y, x + y) = (x, x) + 2(x, y) + (y, y) = || x ||2 + || y ||2

Приведем пример условия ортогональности двух векторов X и Y в пространстве An

X1y1 + x2y2 + … + xnyn = 0

Вспомним, что это условие ортогональности двух векторов, которое в векторной алгебре мы получим из скалярного произведения.

В пространстве c(a, b) условие ортогональности имеет вид

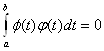
Например, векторы x = cos nt и y = sin mt, где m и n – целые, ортогональны при a = - p и b = p

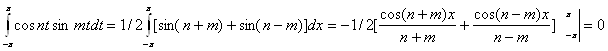
С этим важным примером мы будем часто встречаться в математике.

Теперь введем определение: линейное пространство R называется нормированным, если выполнены следующие два требования:

1. любому элементу x пространства ставится в соответствие или определяется норма .

2. Указанное правило введения нормы подчинено следующим аксиомам:

10 || x || > 0, если x ¹ 0; || x || = 0, если x = 0

20 ||l x || = |l|×|| x ||.

30 справедливо равенство || x + y || £ || x || + || y || называемое неравенством Минковского или неравенством треугольника.

Всякое евклидово пространство является нормированным, если в нем норму любого элемента х определить равенством . Первые две аксиомы непосредственно вытекают из аксиом скалярного произведения 30 и 40.

Справедливость неравенства Минковского докажем, опираясь на неравенство Коши – Буняковского:

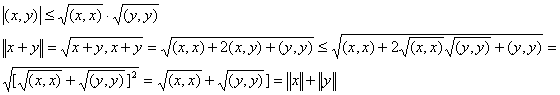
< Предыдущая		Следующая >