57. Евклидовы пространства
Из курса аналитической геометрии нам знакомо понятие скалярного произведения векторов. На прошлой лекции мы ввели понятие линейного пространства. Введем теперь в рассмотрение линейное пространство, для элементов которого каким либо способом определено правило, ставящее в соответствие двум элементам число, называемое Скалярным произведением. Такие пространства называются евклидовыми линейными пространствами.
Определение евклидового пространства. Линейное пространство R называется евклидовым пространством, если выполнены два требования:
1. Имеется правило, посредством которого любым двум элементам этого пространства X и Y ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначается символом (x, y).
2. Указанное правило подчинено следующим четырем аксиомам:
10 (x, y) = (y, x) – переместительное свойство (или симметрия).
20 (x1 + x2, y) = (x1, y) + (x2, y) (распределительное свойство).
30 (l x, y) = l (x, y) (для любого вещественного l).
40 (x, x) > 0, если x ¹ 0 и (x, x) = 0, если x = 0.
Пример 1. Рассмотрим пространство V3 всех свободных векторов. Скалярное произведение определим, как это сделано было в аналитической геометрии. Все аксиомы 10 - 40 при введенном нами ранее определении скалярного произведения
![]()
Будут выполняться. Стало быть, линейное пространство V3 со скалярным произведениям – евклидово пространство.
Пример 2. Рассмотрим бесконечно – мерное пространство C[a, b] всех функций a £ t £ b. Скалярное произведение определим как интеграл от этих функций в пределах от a до b:
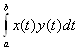
Можно проверить справедливость аксиом 10 - 40. Т. е. это бесконечно - мерное евклидово пространство.
Пример 3. Рассмотрим линейное пространство An упорядоченных совокупностей n вещественных чисел - пространство координат элементов. Положим
X = ( x1 x2 x3 … xn )
Y = ( y1 y2 y3 … yn )
Тогда введением скалярного произведения в виде
(x, y) = x1y1 + x2y2 + …+ xn yn
Можно получить, как не трудно убедиться, евклидово пространство. Определим несколько шире скалярное произведение.
Пример 4. Рассмотрим квадратную матрицу порядка n:
 (*)
(*)
С помощью этой матрицы составим однородный многочлен второго порядка относительно переменных x1, x2, …, xn
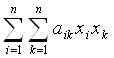
Такой многочлен называется квадратичной формой, порождаемой квадратной матрицей А (*). Квадратичная форма называется положительно определенной, если она принимает строго положительные значения для всех значений переменных, одновременно не равных нулю и равна нулю лишь при условии, что x1 = x2 = … = xn = 0. Потребуем, чтобы матрица А удовлетворяла двум условиям:
10 порождала положительно определенную квадратичную форму
20 была симметричной относительно числовой диагонали, т. е. aik = aki для всех i = 1, 2, …, n ; k = 1, 2, …, n. С помощью матрицы, удовлетворяющей двум этим условиям, определим скалярное произведение двух элементов пространства An
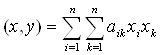 (**)
(**)
Посмотрим на аксиомы 20 и 30 . Они, очевидно, удовлетворяются при совершенной произвольной матрице A. Справедливость 10 вытекает из симметричности матрицы, а 40 – квадратичная форма матрицы А – положительно определенная. Т. о. пространство An со скалярным произведением, определяемым равенством (**) при условиях 10 и 20 , налагаемых на матрицу А, является евклидовым пространством. Если в качестве матрицы А взять единичную матрицу, то мы получим евклидово пространство, рассмотренное в примере 3, обозначаемое как Еn.
| < Предыдущая | Следующая > |
|---|