56. Замена базиса

Рассмотрим линейное преобразование координат некоторого вектора при смене базиса. Предположим, что мы имеем два базиса произвольного n – мерного пространства и . Очевидно, координаты векторов одного базиса можно выразить через другой базис:

(*)

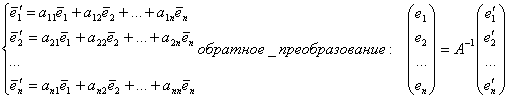В матричном виде:

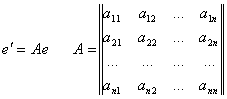
Где матрица А – это матрица, связывающая новый базис ЕI’ со старым Ei.

Рассмотрим некоторый вектор

Подставим здесь вместо их выражения из (*):

Приравнивая здесь коэффициенты при одинаковых векторах , приходим к системе уравнений:

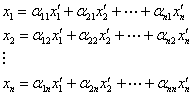
Или в матричном виде

Матрица АТ, транспонированная к А, называется матрицей перехода от одного базиса к другому. Столбцами этой матрицы являются координаты новых базисных векторов в старом базисе. Очевидно, обратный переход есть: X’=(A –1)TX

Вывод: если переход от первого базиса ко второму осуществляется с помощью невырожденной матрицы А, то переход от координат произвольного элемента относительно первого базиса к координатам этого элемента относительно второго базиса осуществляется с помощью транспонированной обратной матрицы.

Пример: в пространстве V3 имеем два базиса:

Найти координаты в базисе . Т. е. . Матрица перехода от базиса к базису есть:

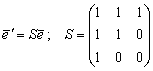Матрица S невырожденная, т. е. система векторов образует базис.

Имеем . Отсюда . Запишем без вычислений, что 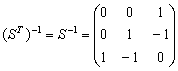. Тогда .

Т. е.

В заключении рассмотрим пространства решений линейной однородной системы. Если решений множество, то известно, что сумма каких-либо решений тоже является решением и произведение каких-либо решений на число тоже является решением. Аксиомы 10 – 80 тоже выполняются. Т. е. множество решений линейной однородной системы являются линейным пространством. Существует Теорема: размерность пространства решений линейной однородной системы уравнений с N неизвестными равна N-R, где R – ранг матрицы системы.

X = Cr+1X1+ Cr+2X2 + … + CnXn-r

Это означает, что решения X1 … Xn-r – линейно независимы и их можно принять за базис пространства решений. Любой базис решений называется фундаментальной системой решений.

< Предыдущая		Следующая >