49. Нецентральные поверхности второго порядка
Очевидно, нецентральная поверхность имеет уравнение:
A11 x2 + a22 y2 + a33 z2 + 2 a14 x + 2 a24 y + 2 a34 z + a44 = 0
Поскольку I3 = 0, то один из A11 A22 A33 должен быть равен 0. Положим, что это a33:
A11 x 2 + a22 y 2 + 2 a14 x + 2 a24 y + 2 a34 z + a44 = 0
Перейдем к новым координатам: 
![]()
И т. д., т. е. избавиться от линейных слагаемых по Х и по У и свести уравнение к виду ![]() . Не нарушая общности, можно считать, что уравнение поверхности есть:
. Не нарушая общности, можно считать, что уравнение поверхности есть: ![]() Здесь могут представиться следующие случаи:
Здесь могут представиться следующие случаи:
А). Если P = Q = 0, то 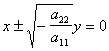 .
.
Поверхность распадается на пару плоскостей, причем, эти плоскости вещественны, когда знаки у A11 И A22 Противоположны.
Б). Р = 0 q ¹ 0
![]()
Это уравнение цилиндра, с образующими, параллельными оси OZ. Причем цилиндр вещественен, если коэффициенты различных знаков.
Здесь также два случая:
5).![]() - это эллиптический цилиндр.
- это эллиптический цилиндр.
6).![]() - это гиперболический цилиндр.
- это гиперболический цилиндр.
В). P ¹ 0 тогда параллельным переносом ![]() можно свести уравнение к виду:
можно свести уравнение к виду: ![]() , или опять можно считать
, или опять можно считать ![]() Здесь в зависимости от знаков могут быть два случая:
Здесь в зависимости от знаков могут быть два случая:
7). ![]() - эллиптический параболоид.
- эллиптический параболоид.
8). ![]() - гиперболический параболоид.
- гиперболический параболоид.
Предположим, что в уравнении
A11 x2 + a22 y2 + a33 z2 + 2 a14 x + 2 a24 y + 2 a34 z + a44 = 0
Две константы A11 и A22 Равны нулю. Тогда перейдем к новым координатам по формулам X = X’ Y = Y’ ![]()
Уравнение сводится к следующему:
A33 Z2 + 2 P X + 2 Q Y + R = 0
А). Если p = 0 q = 0 , то поверхность распадается на две плоскости 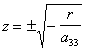
Б). Если хотя бы один из коэффициентов отличен от нуля, то уравнение можно свести к виду
9). A33 Z2 + 2 P Y = 0
Это уравнение параболического цилиндра с образующими, параллульными оси OX.
| < Предыдущая | Следующая > |
|---|