50. Исследуем формы поверхностей второго порядка

1. Эллипсоид.

Из этого уравнения вытекает, что центром симметрии эллипса является начало координат. A, B, C – полуоси эллипса. Для наглядного представления можно выделить плоскость, к примеру Z = H:

или , а это эллипс с полуосями A* и B*:

А*2=а2 /(1- H2 /C2 ) К сведению: земной шар на самом деле не шар, т. к. за счет центробежной силы радиус Земли на полюсах меньше, чем на экваторе и фигура Земли ближе к так называемому эллипсоиду вращения:

2. Гиперболоиды.

 

 

 

 

 

 

 

 

1). Однополостный гиперболоид:

Cечение однополостного гиперболоида координатными плоскостями: XOZ:

- гипербола.

YOZ:

- гипербола. Плоскостью XOY:

- горловой эллипс.

Т. е. начало координат – это центральная точка, координатные плоскости – это плоскости симметрии.

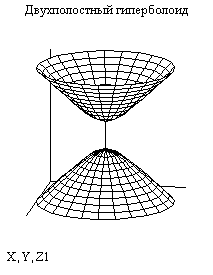2). Двуполостной гиперболоид.

Начало координат – точка симметрии.

Координатные плоскости – плоскости симметрии.

Плоскость Z = H пересекает гиперболоид по эллипсу ,

Т. е. плоскость Z = H начинает пересекать гиперболоид при | H | ³ C. Сечение гиперболоида плоскостями X = 0 и Y = 0 - это гиперболы.

3. Параболоиды.

 

1). Нецентральная поверхность – эллиптический параболоид:

Сечение плоскостью Z = H есть , где . Из уравнения видно, что z ³ 0 – это бесконечная чаша.

Пересечение плоскостями Y = H и X=H - это парабола и вообще, эллиптический параболоид образуется путем параллельного переноса параболы , когда ее вершина движется вдоль параболы , Y = 0, представляющей собой сечение эллиптического параболоида плоскостью Y = 0. Аналогично, можно сказать и относительно плоскости Х= 0.

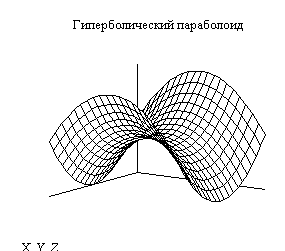
2). Гиперболический параболоид:

 

Очевидно, плоскости XOZ и YOZ – плоскости симметрии, ось z – ось параболоида. Пересечение параболоида с плоскостью Z = H – гиперболы: , . Плоскость Z=0 пересекает гиперболический параболоид по двум осям которые являются ассимптотами.

Можно убедиться, что гиперболический параболоид образуется путем параллельного переноса параболы, образованной пересечением поверхности плоскостью XOZ вдоль параболы, образованной пересечением поверхноcти с плоскостью YOZ.

4. Конус и цилиндры второго порядка.

 

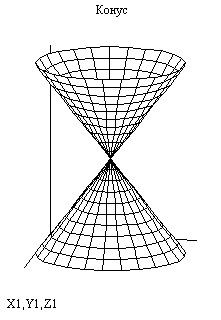1). Конус – это поверхность . Конус оюразован прямыми линиями, проходящими через начало координат 0 ( 0, 0, 0 ). Сечение конуса – это эллипсы с полуосями .

2). Цилиндры второго порядка. Это эллиптический цилиндр .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Гиперболический цилиндр:

 

 

 

 

 

 

 

 

 

Параболический цилиндр:

 

 

 

 

 

 

 

 

 

< Предыдущая		Следующая >