45. Преобразование декартовых прямоугольных координат в пространстве

В пространстве, рассуждая аналогичным образом, можно записать:

(***)

И для координат получить:

(****)

Итак, каковы бы ни были две произвольные системы координат в пространстве, координаты x y z некоторой точки относительно первой системы являются линейными функциями координат X’ Y’ Z’ этой же точки относительно второй системы координат.

Умножая каждое из равенств (***) скалярно на I’ J’ K’ получаем:

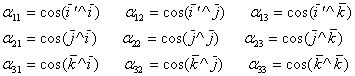
Выясним геометрический смысл формул преобразования (****). Для этого предположим, что обе системы имеют общее начало: A = B = C = 0.

Введем в рассмотрение три угла, полностью характеризующих расположение осей второй системы относительно первой.

Первый угол – образован осью х и осью u, являющейся пересечением плоскостей xOy и x’Oy’. Направление угла – кратчайший поворот от оси x к y. Обозначим угол через y. Второй угол q – это не превосходящий p угол между осями Oz и Oz’. Наконец, третий угол j – это угол между осью u и Ox’, отсчитываемый от оси u в направлении кратчайшего поворота от Ox’ к Oy’. Эти углы называются углами Эйлера.

Преобразование первой системы во вторую можно представить в виде последовательного проведения трех поворотов: на угол y относительно оси Oz; на угол q относительно оси Ox’; и на угол j относительно оси Oz’.

Числа aij можно выразить через углы Эйлера. Эти формулы мы записывать не будем из-за громоздкости.

Само преобразование представляет собой суперпозицию параллельного переноса и трех проводимых последовательных поворотов на углы Эйлера.

Все эти рассуждения можно провести и для случая, когда обе системы левые, или разной ориентации.

Если имеем две произвольные системы, то, вообще говоря, можно их совместить путем параллельного переноса и одного поворота в пространстве вокруг некоторой оси. Искать ее не будем.

< Предыдущая		Следующая >